下列有关行星运动的说法中,正确的是( )
A.由ω=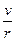 知,行星轨道半径越大,角速度越小 知,行星轨道半径越大,角速度越小 |
| B.由a=rω2知,行星轨道半径越大,行星的加速度越大 |
C.由a=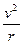 知,行星轨道半径越大,行星的加速度越小 知,行星轨道半径越大,行星的加速度越小 |
D.由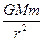 =m =m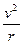 知,行星的轨道半径越大,线速度越小 知,行星的轨道半径越大,线速度越小 |
关于万有引力定律应用于天文学研究的历史事实,下列说法中正确的是( )
| A.天王星、海王星和冥王星都是运用万有引力定律,经过大量计算以后而发现的 |
| B.在18世纪已发现的7个行星中,人们发现第七颗行星——天王星的运动轨道总是同根据万有引力定律计算出来的理论轨道有较大的偏差,于是有人推测,在天王星轨道之外还有一个行星,是它的存在引起了上述偏差 |
| C.海王星是牛顿运用了万有引力定律经过大量计算而发现的 |
| D.冥王星是英国剑桥大学的学生亚当斯和勒维列合作研究后共同发现的 |
利用下列哪组数据,可以计算出地球的质量( )
| A.地球的半径R地和地面的重力加速度g |
B.卫星绕地球做匀速圆周运动的半径R和周期T |
C.卫星绕地球做匀速圆周运动的半径R和线速度v |
D.卫星绕地球做匀速圆周运动的线速度v和周期T |
一飞船在某行星表面附近沿圆轨道绕该行星飞行,认为行星是密度均匀的球体,要确定该行星的密度,只需要测量( )
| A.飞船的轨道半径 |
| B.飞船的运行速度 |
| C.飞船的运行周期 |
| D.行星的质量 |
已知地球半径为6.4×106 m,又知月球绕地球的运动可近似看作匀速圆周运动,则可估算出月球到地心的距离为________________m(结果只保留一位有效数字).
设想人类开发月球,不断把月球上的矿藏搬运到地球上,假定经过长时间开采后,月球仍可看作是均匀的球体,月球仍沿开采前的圆周轨道运动,则与开采前相比( )
| A.地球与月球间的万有引力将变大 |
| B.地球与月球间的万有引力将变小 |
| C.月球绕地球运动的周期将变长 |
| D.月球绕地球运动的周期将变短 |
若已知行星绕太阳公转的半径为r,公转的周期为T,万有引力常量为G,则可求出( )
| A.某行星的质量 |
| B.太阳的质量 |
| C.某行星的密度 |
| D.太阳的密度 |
在研究宇宙发展演变的理论中,有一种学说叫“宇宙膨胀说”,这种学说认为引力常量G在缓慢地减小.根据这一理论,在很久很久以前,太阳系中地球的公转情况与现在相比( )
| A.公转半径R较大 | B.公转周期T较小 |
| C.公转速率v较大 | D.公转角速度ω较小 |
已知地球的半径R≈6.4×106m,地球表面的重力加速度g≈10m/s2,万有引力恒量G≈6.7×10-11N·kg2/m2。由此推导并估算:(把结果只保留一位有效数字即可)
(1)地球的质量M约为多少?
(2)近地环绕卫星的最大线速度v1约为多少?
已知太阳光从太阳射到地球,需要8分20秒,地球公转轨道可近似看成固定圆轨道,地球半径约为6.4×106 m, 试估算太阳质量M与地球质量m之比M/m为多少?(保留一位有效数字)
某行星昼夜转动时间T0=8h,若用一弹簧测力计去测量同一物体的重力,结果在行星赤道上比它在两极处小9﹪.设想该行星自转角速度加快,在赤道上的物体将完全失重.则此行星自转周期多大?(行星看作标准球体)
在一个行星上,一昼夜的时间为T0="6" h。若在行星上用弹簧秤测同一物体的重力,发现在赤道上仅为在两极的90%.设想该行星的自转角速度加快到某一值时,赤道上的物体会自动飘起来.试计算这时行星上的一昼夜是多长?
静电场与引力场有着非常相似的性质,力的形式都遵从平方反比定律,解答下列问题:
(1)写出万有引力定律和库仑定律中的常数G与K的单位。
(2)某星球的质量为M,在该星球表面某一倾角为θ的山坡上以初速度v0平抛一个物体,经 时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)?
时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)?
(3)如图所示,质量为m的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电量为q,在杆上B点处固定一个电量为Q的正电荷。将A由距B竖直高度为H处无初速释放,小球A下滑过程中电量不变。不计A与细杆间的摩擦,整个装置处在真空中。已知静电力恒量k和重力加速度g,求:A球刚释放时的加速度以及当A球的动能最大时,A球与B点的距离。
试题篮
()