理论研究表明第二宇宙速度是第一宇宙速度的 倍。火星探测器悬停在距火星表面高度为h处时关闭发动机,做自由落体运动,经时间t落到火星表面。已知引力常量为G,火星的半径为R。若不考虑火星自转的影响,要使探测器脱离火星飞回地球,则探测器从火星表面的起飞速度至少为
倍。火星探测器悬停在距火星表面高度为h处时关闭发动机,做自由落体运动,经时间t落到火星表面。已知引力常量为G,火星的半径为R。若不考虑火星自转的影响,要使探测器脱离火星飞回地球,则探测器从火星表面的起飞速度至少为
A. |
B. |
C.11.2km/s | D.7.9km/s |
有人设想:可以在飞船从运行轨道进入返回地球程序时,借飞船需要减速的机会,发射一个小型太空探测器,从而达到节能的目的。如图所示,飞船在圆轨道Ⅰ上绕地球飞行,其轨道半径为地球半径的k倍(k>1)。当飞船通过轨道Ⅰ的A点时,飞船上的发射装置短暂工作,将探测器沿飞船原运动方向射出,并使探测器恰能完全脱离地球的引力范围,即到达距地球无限远时的速度恰好为零,而飞船在发射探测器后沿椭圆轨道Ⅱ向前运动,其近地点B到地心的距离近似为地球半径R。以上过程中飞船和探测器的质量均可视为不变。已知地球表面的重力加速度为g。
(1)求飞船在轨道Ⅰ运动的速度大小;
(2)若规定两质点相距无限远时引力势能为零,则质量分别为M、m的两个质点相距为r时的引力势能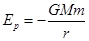 ,式中G为引力常量。在飞船沿轨道Ⅰ和轨道Ⅱ的运动过程,其动能和引力势能之和保持不变;探测器被射出后的运动过程中,其动能和引力势能之和也保持不变。
,式中G为引力常量。在飞船沿轨道Ⅰ和轨道Ⅱ的运动过程,其动能和引力势能之和保持不变;探测器被射出后的运动过程中,其动能和引力势能之和也保持不变。
①求探测器刚离开飞船时的速度大小;
②已知飞船沿轨道Ⅱ运动过程中,通过A点与B点的速度大小与这两点到地心的距离成反比。根据计算结果说明为实现上述飞船和探测器的运动过程,飞船与探测器的质量之比应满足什么条件。
《科学》介绍了一种新技术——航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统。飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等。该系统的工作原理可用物理学的基本定律来解释。
下图为飞缆系统的简化模型示意图,图中两个物体P,Q的质量分别为mP、mQ,柔性金属缆索长为l,外有绝缘层,系统在近地轨道作圆周运动,运动过程中Q距地面高为h。设缆索总保持指向地心,P的速度为vP。已知地球半径为R,地面的重力加速度为g。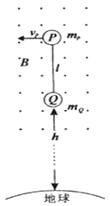
(1)飞缆系统在地磁场中运动,地磁场在缆索所在处的磁感应强度大小为B,方向垂直于纸面向外。设缆索中无电流,求缆索P、Q哪端电势高?两端的电势差多大?
(2)设缆索的电阻为R1,如果缆索两端物体P、Q通过周围的电离层放电形成电流,相应的电阻为R2,求缆索所受的安培力多大?
(3)求缆索对Q的拉力FQ多大?
如图所示,太阳和地球组成“日地双星系统”,两者绕共同的圆心 点(图中未画出)做周期相同的圆周运动.数学家拉格朗日发现,处在拉格朗日点(如图所示)的航天器在太阳和地球引力的共同作用下可以绕“日地双星系统”的圆心
点(图中未画出)做周期相同的圆周运动.数学家拉格朗日发现,处在拉格朗日点(如图所示)的航天器在太阳和地球引力的共同作用下可以绕“日地双星系统”的圆心 点做周期相同的圆周运动,从而使日、地、航天器三者在太空的相对位置保持不变.不考虑航天器对日地双星系统的影响,不考虑其它天体对该系统的影响.已知:太阳质量为
点做周期相同的圆周运动,从而使日、地、航天器三者在太空的相对位置保持不变.不考虑航天器对日地双星系统的影响,不考虑其它天体对该系统的影响.已知:太阳质量为 ,地球质量为
,地球质量为 ,太阳与地球球心距离为
,太阳与地球球心距离为 .则下列说法正确的是
.则下列说法正确的是
A.位于拉格朗日点的绕 点稳定运行的航天器,其向心加速度小于地球的向心加速度 点稳定运行的航天器,其向心加速度小于地球的向心加速度 |
B.日地双星系统的周期为 |
C.圆心 点在太阳和地球的连线上,距离太阳和地球球心的距离之比等于太阳和地球的质量之比 点在太阳和地球的连线上,距离太阳和地球球心的距离之比等于太阳和地球的质量之比 |
D.拉格朗日点距地球球心的距离 满足关系式 满足关系式 |
假设有一载人宇宙飞船在距地面高度为4200km 的赤道上空绕地球做匀速圆周运动,地球半径约为6400km,地球同步卫星距地面高度为36000km,宇宙飞船和地球同步卫星绕地球同向运动,每当二者相距最近时,宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻二者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为 ( )
| A.4次 | B.6次 | C.7次 | D.8次 |
长期以来“卡戎星”被认为是冥王星唯一的卫星,它的公转轨道半径r1≈2.0×104km,公转周期T1≈6天。2006年3月,天文学家新发现两颗冥王星的小卫星,其中一颗的公转轨道半径r2≈4.8×104km,取 ,则它的公转周期T2最接近于 ( )
,则它的公转周期T2最接近于 ( )
| A.11天 | B.23天 | C.35天 | D.83天 |
英国某媒体推测:在2020年之前,人类有望登上火星,而登上火星的第一人很可能是中国人。假如你有幸成为人类登陆火星的第一人,乘坐我国自行研制的、代表世界领先水平的神舟x号宇宙飞船,通过长途旅行,可以亲眼目睹了美丽的火星。为了熟悉火星的环境,你的飞船绕火星做匀速圆周运动,离火星表面的高度为H,飞行了n圈,测得所用的时间为t.已知火星半径为R,试求火星表面重力加速度g.
2013年12月2日凌晨2时17分,“嫦娥三号”由“长征三号乙”运载火箭成功送入太空,经过一系列的调控和变轨,“嫦娥三号”最终顺利降落在月球表面,如图所示.“嫦娥三号”在地月转移轨道的P点调整后进入环月圆形轨道1,进一步调整后进入环月椭圆轨道2.有关“嫦娥三号”下列说法正确的是( )
| A.在P点由轨道1进入轨道2需要减速 |
| B.在地球上的发射速度一定大于第二宇宙速度 |
| C.在轨道2经过P点时速度大于Q点速度 |
| D.分别由轨道1与轨道2经P点时,向心加速度相同 |
太阳系个行星几乎在同一平面内沿同一方向绕太阳做圆周运动,当地球恰好运行到某个行星和太阳之间,且三者几乎成一条直线的现象,天文学成为"行星冲日"据报道,2014年各行星冲日时间分别是:1月6日,木星冲日,4月9日火星冲日,6月11日土星冲日,8月29日,海王星冲日,10月8日,天王星冲日,已知地球轨道以外的行星绕太阳运动的轨道半径如下表所示,则下列判断正确的是:()
| 地球 |
火星 |
木星 |
土星 |
天王星 |
海王星 |
|
| 轨道半径(AU) |
1.0 |
1.5 |
5.2 |
9.5 |
19 |
30 |
| A. |
各点外行星每年都会出现冲日现象 |
| B. |
在2015年内一定会出现木星冲日 |
| C. |
天王星相邻两次的冲日的时间是土星的一半 |
| D. |
地外行星中海王星相邻两次冲日间隔时间最短 |
石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖。用石墨烯制作超级缆绳,人类搭建"太空电梯"的梦想有望在本世纪实现。科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换。

(1)若"太空电梯"将货物从赤道基站运到距地面高度为的同步轨道站,求轨道站内质量为
的货物相对地心运动的动能。设地球自转角速度为
,地球半径为
。
(2)当电梯仓停在距地面高度的站点时,求仓内质量
的人对水平地板的压力大小。取地面附近重力加速度
,地球自转角速度
,地球半径
。
已知地球的自转周期和半径分别为和
,地球同步卫星
的圆轨道半径为
。卫星B沿半径为
的圆轨道在地球赤道的正上方运行,其运行方向与地球自转方向相同。求:
(1)卫星做圆周运动的周期;
(2)卫星和
连续地不能直接通讯的最长时间间隔(信号传输时间可忽略)。
万有引力定律揭示了天体运动的规律与地上物体运动规律具有内在的一致性。
(1)用弹簧秤称量一个相对于地球静止的小物体的重量,随称量位置的变化可能会有不同的结果。已知地球的质量为,自转周期为
,引力常量为
。将地球看作是半径为
,质量均匀分布的球体,不考虑空气的影响。设在地球北极地面称量时,弹簧秤的读数
。
a.若在北极上空处称量,弹簧秤的读数为
,求比值
的表达式(并就
的情形算出具体数值,(计算结果保留两位有效数字)
b.若在赤道地面处称量,弹簧秤的读数为,求比值
的表达式
(2)设想地球绕太阳公转的半径为,太阳的半径为
,地球的半径为
,三者均减小为现在的1.0%,太阳和地球的密度均匀且不变,仅考虑太阳和地球之间的相互作用,以现实地球的1年为标准,计算"设想地球"的一年将变为多长?
两个星球组成双星,它们在相互之间的引力作用下,绕连线上的某点做周期相同的匀速圆周运动.现测得两星中心距离为L,其运动周期为T,万有引力常量为G,则两星各自的圆周运动半径与其自身的质量成 (填“正比”或者“反比”);两星的总质量为 。
教科版高中物理教材必修2中介绍, ,亚当斯通过对行星“天王星”的长期观察发现,其实际运行的轨道与圆轨道存在一些偏离,且每隔时间t发生一次最大的偏离。亚当斯利用牛顿发现的万有引力定律对观察数据进行计算, 认为形成这种现象的原因可能是天王星外侧还存在着一颗未知行星(后命名为海王星),它对天王星的万有引力引起其轨道的偏离。由于课本没有阐述其计算的原理,这极大的激发了树德中学天文爱好社团的同学的探索热情,通过集体研究,最终掌握了亚当斯当时的计算方法:设其(海王星)运动轨道与天王星在同一平面内,且与天王星的绕行方向相同,天王星的运行轨道半径为R,周期为T,并认为上述最大偏离间隔时间t就是两个行星相邻两次相距最近的时间间隔,并利用此三个物理量推导出了海王星绕太阳运行的圆轨道半径,则下述是海王星绕太阳运行的圆轨道半径表达式正确的是( )
A. |
B. |
C. |
D. |
试题篮
()