假设某星球表面上有一倾角为 的固定斜面,一质量为
的固定斜面,一质量为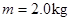 的小物块从斜面底端以速度9m/s沿斜面向上运动,小物块运动1.5s时速度恰好为零.已知小物块和斜面间的动摩擦因数为0.25,该星球半径为
的小物块从斜面底端以速度9m/s沿斜面向上运动,小物块运动1.5s时速度恰好为零.已知小物块和斜面间的动摩擦因数为0.25,该星球半径为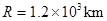 .(
.(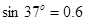 .
.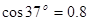 ),试求:
),试求: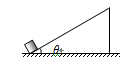
(1)该星球表面上的重力加速度g的大小;
(2)该星球的第一宇宙速度.
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即 =k,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知万有引力常量为G,太阳的质量为M太.
=k,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知万有引力常量为G,太阳的质量为M太.
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立.经测定月球到地球中心距离为3.84×108m,月球绕地球运动的周期为2.36×106s,试计算地球的质量M地.(G=6.67×10-11N·m2/kg2,结果保留一位有效数字)
某宇航员在一星球表面附近高度为H处以速度v0水平抛出一物体,经过一段时间后物体落回星球表面,测得该物体水平位移为x,已知星球半径为R,万有引力常量为G.不计空气阻力,求:
(1)该星球质量M;
(2)该星球第一宇宙速度大小v.
阅读以下信息:
①2013年12月2日1时30分,“嫦娥三号”在西昌卫星发射中心发射,经过19分钟的飞行后,火箭把“嫦娥三号”送入近地点高度210千米、远地点高度约36.8万千米的地月转移轨道。“嫦娥三号”奔月的近似轨迹如图所示。
②经过地月转移轨道上的长途飞行后,“嫦娥三号”在距月面高度约100千米处成功变轨,进入环月圆轨道。在该轨道上运行了约4天后,再次成功变轨,进入近月点高度15千米、远月点高度100千米的椭圆轨道。
③2013年12月14日晚21时,随着首次应用于中国航天器的空间变推力发动机开机,沿椭圆轨道通过近月点的“嫦娥三号”从每秒钟1.7千米的速度实施动力下降。
④2013年12月14日21时11分,“嫦娥三号”成功实施软着陆。
⑤开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即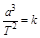 ,k是一个对所有行星都相同的常量。该定律适用于一切具有中心天体的引力系统。
,k是一个对所有行星都相同的常量。该定律适用于一切具有中心天体的引力系统。
⑥月球的质量M=7.35×1022kg,半径R=1.74×103km;月球绕地球运行的轨道半长轴a0=3.82×105km,月球绕地球运动的周期T0=27.3d(d表示天);质量为m的物体在距离月球球心r处具有的引力势能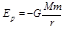 ,引力常量G=6.67×10-11 N·m2/kg2;地球的半径R0=6.37×103km。
,引力常量G=6.67×10-11 N·m2/kg2;地球的半径R0=6.37×103km。
根据以上信息,请估算: 
(1)“嫦娥三号”在100km环月圆轨道上运行时的速率v;
(2)“嫦娥三号”在椭圆轨道上通过远月点时的速率v远;
“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下:如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为 ;石油密度远小于
;石油密度远小于 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。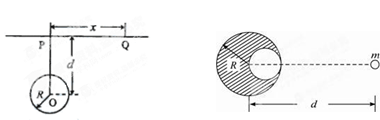
(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径), =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值 (
( 在OP方向上的分量)
在OP方向上的分量)
(3)若在水平地面上半径L的范围内发现:重力加速度反常值在 与
与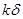 (k>1)(
(k>1)( 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为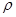 ;石油密度远小于
;石油密度远小于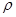 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏高。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏高。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。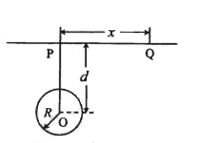
(1)设球形空腔体积为V,球心深度为d(远小于地球半径), =x,求空腔所引起的Q点处的重力加速度反常
=x,求空腔所引起的Q点处的重力加速度反常
(2)若在水平地面上半径L的范围内发现:重力加速度反常值在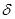 与
与 (k>1)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
(k>1)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
试题篮
()