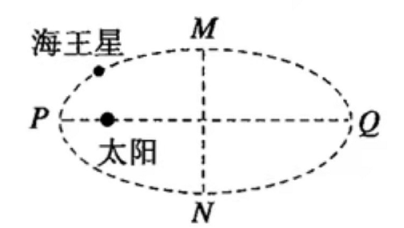
如图,海王星绕太阳沿椭圆轨道运动,P为近日点,Q为远日点,M、N为轨道短轴的两个端点,运行的周期为 T0 。若只考虑海王星和太阳之间的相互作用,则海王星在从P经过M、Q到N的运动过程中( )
| A. |
从P到M所用的时间等于 T0/4 |
| B. |
从Q到N阶段,机械能逐渐变大 |
| C. |
从P到Q阶段,速率逐渐变小 |
| D. |
从M到N阶段,万有引力对它先做负功后做正功 |
静止在水平地面上的两小物块A、B,质量分别为m A=l.0 kg,m B=4.0 kg;两者之间有一被压缩的微型弹簧,A与其右侧的竖直墙壁距离l=1.0m,如图所示。某时刻,将压缩的微型弹簧释放,使A、B瞬间分离,两物块获得的动能之和为E k=10.0 J。释放后,A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为u=0.20。重力加速度取g=10 m/s²。A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短。

(1)求弹簧释放后瞬间A、B速度的大小;
(2)物块A、B中的哪一个先停止?该物块刚停止时A与B之间的距离是多少?
(3)A和B都停止后,A与B之间的距离是多少?
如图,两条光滑平行金属导轨固定,所在平面与水平面夹角为θ , 导轨电阻忽略不计。虚线ab、cd均与导轨垂直,在ab与cd之间的区域存在垂直于导轨所在平面的匀强磁场。将两根相同的导体棒PQ、MN先后自导轨上同一位置由静止释放,两者始终与导轨垂直且接触良好。已知PQ进入磁场开始计时,到MN离开磁场区域为止,流过PQ的电流随时间变化的图像可能正确的是( )
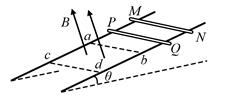
A.  B.
B.  C.
C. 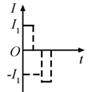 D.
D. 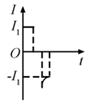
从地面竖直向上抛出一物体,其机械能E 总等于动能E k与重力势能E p之和。取地面为重力势能零点,该物体的E 总和E p随它离开地面的高度h的变化如图所示。重力加速度取10 m/s 2。由图中数据可得( )
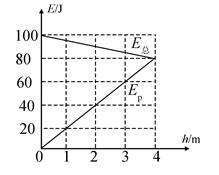
A. 物体的质量为2 kg B. h=0时,物体的速率为20 m/s
C. h=2 m时,物体的动能 E k=40 J D. 从地面至 h=4 m,物体的动能减少100 J
在一斜面顶端,将甲乙两个小球分别以v和
v2 的速度沿同一方向水平抛出,两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的( )
A. 2倍 B. 4倍 C. 6倍 D. 8倍
高空坠物极易对行人造成伤害。若一个50g的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为 2ms ,则该鸡蛋对地面产生的冲击力约为( )
| A. |
10N |
B. |
102N |
C. |
103N |
D. |
104N |
小球P和Q用不可伸长的轻绳悬挂在天花板上,P球的质量大于Q球的质量,悬挂P球的绳比悬挂Q球的绳短.将两球拉起,使两绳均被水平拉直,如图所示.将两球由静止释放.在各自轨迹的最低点,( )

| A. |
P球的速度一定大于Q球的速度 |
B. |
P球的动能一定小于Q球的动能 |
| C. |
P球所受绳的拉力一定大于Q球所受绳的拉力 |
D. |
P球的向心加速度一定小于Q球的向心加速度 |
如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。用力向右推动车厢使弹簧压缩,撤去推力时滑块在车厢底板上有相对滑动。在地面参考系(可视为惯性系)中,从撤去推力开始,小车、弹簧和滑块组成的系统( )

| A. |
动量守恒,机械能守恒 |
| B. |
动量守恒,机械能不守恒 |
| C. |
动量不守恒,机械能守恒 |
| D. |
动量不守恒,机械能不守恒 |
一物块在高 3.0m 、长 5.0m 的斜面顶端从静止开始沿斜面下滑,其重力势能和动能随下滑距离 s 的变化如图中直线Ⅰ、Ⅱ所示,重力加速度取 10m/s2 .则 ( )

| A. |
物块下滑过程中机械能不守恒 |
| B. |
物块与斜面间的动摩擦因数为0.5 |
| C. |
物块下滑时加速度的大小为 6.0m/s2 |
| D. |
当物块下滑 2.0m 时机械能损失了 12J |
如图所示,鼓形轮的半径为 R,可绕固定的光滑水平轴 O转动。在轮上沿相互垂直的直径方向固定四根直杆,杆上分别固定有质量为 m的小球,球与 O的距离均为 2R.在轮上绕有长绳,绳上悬挂着质量为 M的重物。重物由静止下落,带动鼓形轮转动。重物落地后鼓形轮匀速转动,转动的角速度为 ω.绳与轮之间无相对滑动,忽略鼓形轮、直杆和长绳的质量,不计空气阻力,重力加速度为 g。求:
(1)重物落地后,小球线速度的大小 v;
(2)重物落地后一小球转到水平位置 A,此时该球受到杆的作用力的大小 F;
(3)重物下落的高度 h。

试题篮
()