如图所示,质量为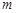 的物块放在弹簧上,与弹簧一起在竖直方向上做简谐运动,当振幅为A时,物体对弹簧的最大压力是物重的
的物块放在弹簧上,与弹簧一起在竖直方向上做简谐运动,当振幅为A时,物体对弹簧的最大压力是物重的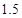 倍,则物体对弹簧的最小压力是多少?要使物体在振动中不离开弹簧,振幅不能超过多大?
倍,则物体对弹簧的最小压力是多少?要使物体在振动中不离开弹簧,振幅不能超过多大?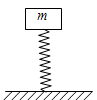
如图所示,让质量m=5.0kg的摆球由图中所示位置A从静止开始下摆,摆至最低点B点时恰好绳被拉断。已知摆线长L=1.6m,悬点O与地面的距离OC=4.0m。若空气阻力不计,摆线被拉断瞬间小球的机械能无损失。(g取10 m/s2)求: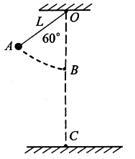
(1)摆线所能承受的最大拉力T;
(2)摆球落地时的动能。
劲度系数为k的轻弹簧上端固定一只质量为m的小球,向下压小球后从静止释放,小球开始做简谐运动。该过程小球的最大加速度是2.8g(g为重力加速度)。求:
⑴简谐运动的振幅大小A;
⑵当小球运动到最低点时,小球对弹簧弹力F的大小和方向;
⑶若弹簧原长为L,则振动过程中弹簧的最大长度L′是多少?
(15分)如图所示,均匀介质中两波源 分别位于x轴上
分别位于x轴上 14m处,质点P位于x轴上
14m处,质点P位于x轴上 4m处,
4m处, 时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源
时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源
 的振幅均为A=2cm,则
的振幅均为A=2cm,则
①经过多长时间,由波源 发出的波到达P点?
发出的波到达P点?
②从 至
至 0.35s内质点P通过的路程多少?
0.35s内质点P通过的路程多少?
如下图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小A孔进入半径R=0.3m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔。已知摆线长L=2m, ,小球质量为m=1kg,D点与小孔A的水平距离s=2m,g取10m/s2。试求:
,小球质量为m=1kg,D点与小孔A的水平距离s=2m,g取10m/s2。试求:
(1)求摆线能承受的最大拉力为多大?
(2)要使摆球能进入圆轨道并且不脱离轨道,求粗糙水平面摩擦因数μ的范围。
竖直悬挂的弹簧振子下端装有记录笔,在竖直面内放置记录纸。当振子上下振动时,以水平向左速度v=10m/s匀速拉动记录纸,记录笔在纸上留下记录的痕迹,建立坐标系,测得的数据如图所示,求弹簧振子振动的振幅和频率。
一列简谐波沿x轴方向传播,已知x轴上x1=0和x2="1" m两处质点的振动图象分别如图(甲)、(乙)所示,
求(1)若此波沿x轴正向传播,则波的传播速度的可能值.
(2)若此波沿x轴负向传播,则波的传播速度的可能值.
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,介质中质点P、Q分别位于x="2" m、x="4" m处.从t=0时刻开始计时,当t="15" s时质点Q刚好第4次到达波峰.
(1)求波速;
(2)写出质点P做简谐运动的表达式.
有一弹簧振子在水平方向上的BC之间做简谐运动,已知BC间的距离为20 cm,振子在2 s内完成了10次全振动.若从某时刻振子经过平衡位置时开始计时(t=0),经过周期振子有正向最大加速度.
(1)求振子的振幅和周期;
(2)在图中作出该振子的位移-时间图象;
(3)写出振子的振动表达式.
一均匀介质中选取平衡位置在同一直线上的9个质点,相邻两质点间的距离均为0.1m,如图(a)所示.一列横波沿该直线向右传播,t=0时到达质点1,质点1开始向下运动,振幅为0.2m,经过时间0.3s,第一次出现如图(b)所示的波形.
①求该列横波传播的速度;
②写出质点1的振动方程;
③在介质中还有一质点P,P点距质点1的距离为10.0m,则再经多长时间P点处于波峰?
有两列简谐横波a、b在同一媒质中沿x轴正方向传播,波速均为v=2.5m/s。在t=0时,两列波的波峰正好在x=2.5m处重合,如图所示。
(1)求两列波的周期Ta和Tb。
(2)求t=0时,两列波的波峰重合处的所有位置。
(1)如图甲所示,M、N是真空中两个电荷量均为+Q的固定点电荷,M、N间的距离为a;沿MN连线的中垂线建立坐标轴,P是x轴上的点,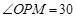 °。已知静电力常量为k。
°。已知静电力常量为k。
a.求P点场强的大小和方向;
b.在图乙中定性画出场强E随x变化的图像(取向右为场强E的正方向)。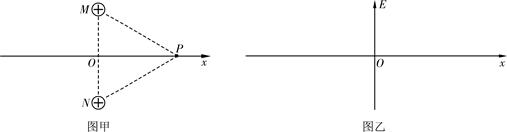
(2)如图丙所示,一个半径为R、电荷量为+Q的均匀带电圆环固定在真空中,环心为O,MN是其中轴线。现让一电荷量为−q、质量为m的带电粒子从MN上的P点由静止释放,P、O间的距离为d。不计粒子重力。试证明:当d<< R时,带电粒子做简谐运动。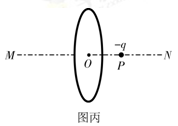
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,介质中质点P、Q分别位于x=2m、x=4m处.从t=0时刻开始计时,当t=15 s时质点Q刚好第4次到达波峰.
(1)求波速;
(2)写出质点P做简谐运动的表达式(不要求推导过程).
竖直悬挂的弹簧振子下端装有记录笔,在竖直面内放置记录纸.当振子上下振动时,以水平向左速度v=10m/s匀速拉动记录纸,记录笔在纸上留下记录的痕迹,建立坐标系,测得的数据如图所示,求振子振动的振幅和频率.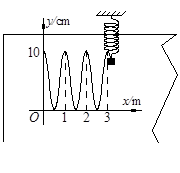
试题篮
()