高中物理* 用三角函数表示简谐运动计算题

弹簧振子以O点为平衡位置，在B、C两点间做简谐运动，在t＝0时刻，振子从O、B间的P点以速度v向B点运动；在t＝0.20 s时，振子速度第一次变为－v；在t＝0.50 s时，振子速度第二次变为－v.
(1)求弹簧振子振动周期T.
(2)若B、C之间的距离为25 cm，求振子在4.00 s内通过的路程．
(3)若B、C之间的距离为25 cm.从平衡位置计时，写出弹簧振子位移表达式，并画出弹簧振子的振动图象．

如图12－1－8所示是某同学设计的测量物体质量的装置，其中P是光滑水平面，N是质量为M的带夹子的金属盒，金属盒两端分别连接轻质弹簧；Q是固定于盒子上的遮光片，利用它和光电计时器能测量金属盒振动时的频率．已知弹簧振子做简谐运动时的周期T＝2π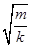，其中m是振子的质量，k 是常数．当空盒振动时，测得振动频率为f₁；把一物体夹在盒中，并使其振动时，测得频率为f₂.你认为这套装置能测量物体的质量吗？如果不能，请说明理由；若能，请求出被测物体的质量．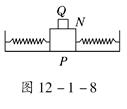

一列简潜横波，如图中的实线是某时刻的波形图象，虚线是经过0.2s时的波形图象。

①假定波向左传播，求它传播的可能距离；
②若这列波向右传播，求它的最大周期：
③假定波速是35m/s，求波的传播方向。

波源S₁和S₂振动方向相同，频率均为4Hz，分别置于均匀介质中轴上的两点处，，如图所示.两波源产生的简谐横波沿轴相向传播，波速为.己知两波源振动的初始相位相同.求：

（1）简谐横波的波长： （2）OA间合振动振幅最小的点的位置。

两块质量分别为m₁、m₂的木板，被一根劲度系数为k轻弹簧连在一起，并在m₁板上加压力F，如图所示，撤去F后，m₁板将做简谐运动。为了使得撤去F后，m₁跳起时恰好能带起m₂板，则所加压力F的最小值为?

一列简谐横波在x轴线上传播着，在t₁=0和t₂=0.005s时的波形曲线如图所示：

⑴横波的波长是多大？振幅A是多大？
⑵设周期大于(t₂ – t₁)，如果波向左传播，波速多大？
⑶设周期小于(t₂ – t₁)，且波速为6800m/s，求波的传播方向.

弹簧振子以O点为平衡位置，在B、C两点间做简谐运动.在t＝0时刻，振子从O、B间的P 点以速度v向B点运动；在t="0.20" s时，振子速度第一次变为-v；在t="0.50" s时，振子速度第二次变为-v.
(1)求弹簧振子振动的周期T；
(2)若B、C之间的距离为25 cm，求振子在4.0 s内通过的路程.

弹簧振子以O点为平衡位置在B、C两点间做简谐运动，B、C相距20 cm，某时刻振子处于B点，经0.5 s振子首次到达C点.求：
(1)振子的振幅、周期；
(2)振子在5 s内通过的路程和5 s末相对平衡位置位移的大小.

如图所示，质量为m＝0.5kg的物体放在质量为M＝4.5kg的平台上，随平台上、下做简谐运动．设在简谐运动过程中，二者始终保持相对静止．已知弹簧的劲度系数为k＝400N/m，振幅为A＝0.1m.。试求：二者一起运动到最低点时，物体对平台的压力大小；(取g＝10m/s)

如图所示是一列沿x轴正方向传播的简谐横波在t =0时刻的波形图，波的传播速度v = 2m/s，试求：

①x =" 4" m处质点的振动函数表达式
② x =" 5" m处质点在0～4．5s内通过的路程s。

光滑圆弧形轨道半径Ｒ＝10m，一小球Ａ自最低点Ｏ开始在槽内做往复运动，当Ａ开始运动时，离Ｏ点的水平距离为Ｓ＝５m处的平台边缘Ｏ^１处另有一小球Ｂ以v的初速度水平抛出，要让Ｂ在Ｏ点处击中Ａ球，则Ｂ球的初速度以及Ｏ^１与Ｏ间的高度差h应满足什么条件？

如图，两根劲度系数分别为K₁、K₂的轻质弹簧与小球相连结，另外一端固定不动。整个装置位于光滑的水平地面上。当小球位于O点时，两弹簧均处于原长状态。今把小球沿弹簧轴线方向拉离O一小段距离后放手。证明小球此后的运动为简谐运动。

如图所示，两物块M、N的质量分别为和，用劲度系数为的足够长的轻弹簧连在一起，放在水平面上，整个系统处于静止状态，现将木块M缓慢下压一端距离后突然释放M，它就上下振动，在振动过程中木块N始终没有离开地面，弹簧的形变量在弹性限度内，求下压距离的最大值。

如图所示的系统中，弹簧的劲度系数为k = 39.2N/m，置于上面的物体质量m = 0.1kg，置于下面的物体质量M = 0.2kg。两物体之间的最大静摩擦力f_max = 0.196N。M与水平面之间是光滑的。若使两物体一起做简谐运动，要求

（1）画出该振动系统在平衡位置时下面物体的受力分析图
（2）该系统振动的最大振幅是多大

如图所示，一列简谐波沿x轴正方向传播，在t₁ = 0.05s和t₂ = 0.1s的波形图如图中的实线和虚线所示。试求

（1）这列波的波长值。（2）这列波的速度可能值。