内壁光滑的导热汽缸竖直浸放在盛有冰水混合物的水槽中,用不计质量的活塞封闭压强为1.0×105 Pa、体积为2.0×10-3 m3的理想气体.现在活塞上方缓缓倒上沙子,使封闭气体的体积变为原来的一半,然后将汽缸移出水槽,缓慢加热,使气体温度变为127℃.(大气压强为1.0×105 Pa)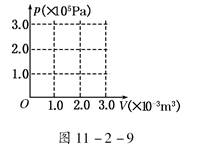
(1)求汽缸内气体的最终体积;
(2)在图11-2-9所示的p-V图上画出整个过程中汽缸内气体的状态变化.
(1)研成粉末后的物体已无法从外形特征和物理性质各向异性上加以判断时,可以通过________________方法来判断它是否为晶体.
(2)在严寒的冬天,房间玻璃上往往会结一层雾,雾珠是在窗玻璃的________________表面.(填“外”或“内”).
(3)密闭容器里液体上方的蒸汽达到饱和后,还有没有液体分子从液面飞出?为什么这时看起来不再蒸发?
答:___________________________________________________________________
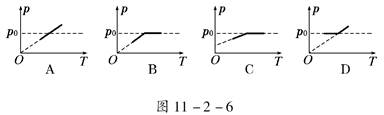
如图11-2-5所示,一向右开口的汽缸放置在水平地面上,活塞可无摩擦移动且不漏气,汽缸中间位置有小挡板.初始时,外界大气压为p0,活塞紧压小挡板处,现缓慢升高缸内气体温度,则如图11-2-6所示的p-T图象能正确反应缸内气体压强变化情况的是 ( )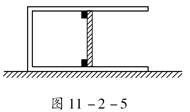
某压力锅结构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。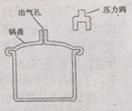
(1)若此时锅内气体的体积为V,摩尔体积为V0,阿伏加德罗常数为NA,写出锅内气体分子数的估算表达式。
(2)假定在一次放气过程中,锅内气体对压力阀及外界做功1J,并向外界释放了2J的热量。锅内原有气体的内能如何变化?变化了多少?
(3)已知大气压强P随海拔高度H的变化满足P=P0(1-αH),其中常数α>0。结合气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度有何不同。
一定质量的气体从外界吸收2.6×105J的热量,内能增加4.2×105J,是气体对外做功还是外界对气体做功?做多少焦耳的功?若气体所吸收热量2.6×105J不变,但内能只增加1.6×105J,情况又如何?
一定质量的理想气体,由初始状态A开始,按图中箭头所示的方向进行了一系列状态变化,最后又回到初始状态A ,即A→B→C→A(其中BC与纵轴平行,CA与横轴平行) ,这一过程称为一个循环,则:
A由A→B,气体分子的平均动能 (填“增大”、“减小”或“不变”)
B由B→C,气体的内能 (填“增大”、“减小”或“不变”)
C由C→A,气体 热量(填 “吸收”或“放出”)
下面关于熵的说法错误的是( )
| A.熵是物体内分子运动无序程度的量度 |
| B.在孤立系统中,一个自发的过程熵总是向减少的方向进行 |
| C.热力学第二定律的微观实质是熵是增加的 |
| D.熵值越大,代表系统分子运动越无序 |
一定质量的理想气体沿如图所示的过程从A变化到B,则在这一过程中气体( ) 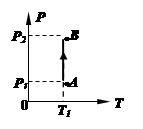
| A.向外界放出热量 |
| B.对外界做了功 |
| C.分子的平均动能增大 |
| D.密度增大 |
喜庆日子,室外经常使用巨大的红色气球来烘托气氛。在晴朗的夏日,对密闭在红色气球内的气体(视为理想气体)从早晨到中午过程,下列说法中正确的是( )
| A.吸收了热量,同时体积膨胀对外做功,内能不变 |
| B.吸收了热量,同时体积膨胀对外做功,内能增加 |
| C.气体密度增加,分子平均动能增加 |
| D.气体密度不变,气体压强不变 |
一定质量的理想气体,体积由V1膨胀到V2,如果是通过等压过程实现,做功为W1、 传递热量为Q1、内能变化为△U1;如果是通过等温过程实现,做功为W2、传递热量为Q2、内能变化为△U2,则
| A.W1>W2,Q1>Q2,△U1>△U2 |
| B.W1>W2,Q1>Q2,△U1=△U2 |
| C.W1>W2,Q1=Q2,△U1>△U2 |
| D.W1<W2,Q1=Q2,△U1=△U2 |
下列说法正确的是 ( )
| A.气体对器壁的压强就是大量气体分子作用在器壁单位面积上的平均作用力 |
| B.气体对器壁的压强就是大量气体分子单位时间作用在器壁上的平均作用力 |
| C.气体分子热运动的平均动能减小,气体的压强一定减小 |
| D.单位体积的气体分子数增加,气体的压强可能增大 |
在各处温度相等的液体中,一个小气泡由液体的底层缓慢地升到液面,上升过程中气泡的体积不断增大,则气泡在浮起过程中( )
| A.放出热量 | B.吸收热量 | C.压强增大 | D.压强减小 |
试题篮
()