高中物理封闭气体压强计算题

一定质量的理想气体由状态A变为状态D，其有关数据如图甲所示，若状态D的压强是2×10⁴Pa 。求
（1）状态A的压强.
（2）请在乙画中出该状态变化过程的P—T图像，并分别标出A、B、C、D各个状态，不要求写出计算过程。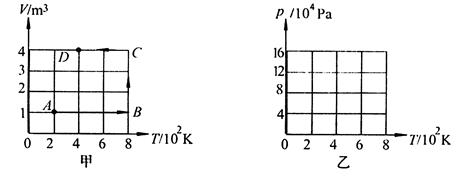

如图，容积为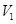的容器内充有压缩空气。容器与水银压强计相连，压强计左右两管下部由软胶管相连。气阀关闭时，两管中水银面同高，左管中水银面上方到气阀之间空气的体积为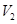。打开气阀，左管中水银下降；缓慢地向上提右管，使左管中水银面回到原来高度，此时右管与左管中水银面的高度差为h。已知水银的密度为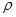，大气压强为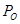，重力加速度为g；空气可视为理想气体，其温度不变。求气阀打开前容器中压缩空气的压强P₁。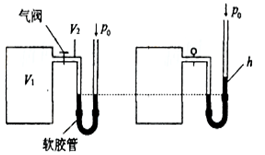

一定质量的理想气体在某一过程中，外界对气体做功7.0×10⁴ J，气体内能减少1.3×10⁵ J，此过程中
（1）气体从外界吸热还是对外放热？
(2）求吸收或者放出的热量为多少？

今有一质量为M的气缸，用质量为m的活塞封有一定质量的理想气体，当气缸水平横放时，空气柱长为L₀（如图甲所示），若将气缸按如图乙悬挂保持静止时，求气柱长度为多少？已知大气压强为P₀，活塞的横截面积为S，它与气缸之间无摩擦且不漏气，且气体温度保持不变.

如图是用导热性能良好的材料制成的气体实验装置，周围温度不变，开始时封闭的空气柱长度为3cm，此时气压表显示容器内压强为p₁=1.0×10⁵Pa，现在将活塞缓慢向下推动，直到封闭空气柱长度变为2 cm．g=10m/s²．问：
(1)最终气压表的示数是多少?
(2)若快速压缩气体过程中，气体内能增加1.5 J，气体放出的热量为1.4J，那么活塞对气体做功是多少?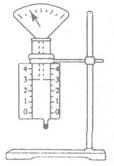

如图，圆柱形气缸的上部有小挡板，可以阻止活塞滑离气缸，气缸内部的高度为d，质量不计的薄活塞将一定质量的气体封闭在气缸内．开始时活塞离底部高度为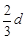，温度为t₁=27℃，外界大气压强为p₀=1atm，现对气体缓缓加热．求：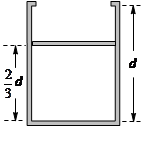

（1）气体温度升高到t₂=127℃时，活塞离底部的高度；
（2）气体温度升高到t₃=357℃时，缸内气体的压强；

如图所示，粗细均匀、导热良好、装有适量水银的U型管竖直放置，右端与大气相通，左端封闭气柱长（可视为理想气体），两管中水银面等高。先将右端与一低压舱（未画出）接通，稳定后右管水银面高出左管水银面（环境温度不变，大气压强）

①求稳定后低压舱内的压强（用""做单位）

②此过程中左管内的气体对外界（填"做正功""做负功""不做功"），气体将（填"吸热"或放热"）。

内壁光滑的导热气缸开口向上竖直浸放在盛有冰水混合物的水槽中，用不计质量的活塞封闭着体积为2.73×10^-3m³的理想气体，活塞面积为2.00×10^-4m²。现在活塞上方缓缓倒上砂子，使封闭气体的体积变为原来的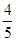，然后将气缸移出水糟，缓缓加热，使气体体积重新变为2.73×10^-3m³（大气压强p₀=1.00×10⁵Pa，g=10m/s²）。求：
①所加砂子的质量；
②气缸内气体最终的温度。

在如图所示的坐标系中，一定质量的某种理想气体先后发生以下两种状态变化过程：第一种变化是从状态状态A到状态B，外界对该气体做功为6J；第二种变化是从状态A到状态C，该气体从外界吸收的热量为9J。图线AC的反向延长线通过坐标原点O，B、C两状态的温度相同，理想气体的分子势能为零。求：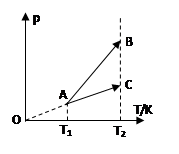

（1）从状态A到状态C的过程，该气体对外界做的功 W₁和其内能的增量；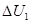
（2）从状态A到状态B的过程，该气体内能的增量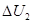及其从外界吸收的热量Q₂。

为适应太空环境，去太空旅行的航天员都要穿航天服。航天服有一套生命系统，为航天员提供合适的温度、氧气和气压，让航天员在太空中如同在地面上一样。假如在地面上航天服内气压为1．0×10⁵Pa，气体体积为2L，到达太空后由于外部气压低，航天服急剧膨胀，内部气体体积变为4L，使航天服达到最大体积。若航天服内气体的温度不变，将航天服视为封闭系统。
①求此时航天服内的气体压强；
②若开启航天服封闭系统向航天服内充气，使航天服内的气压恢复到9．0×10⁴ Pa，则需补充1．0×10⁵ Pa的等温气体多少升？

如图，在大气中有一水平放置的固定圆筒，它由a、b和c三个粗细不同的部分连接而成，各部分的横截面积分别为2S、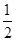S和S。已知大气压强为p₀，温度为T₀.两活塞A和B用一根长为4l的不可伸长的轻线相连，把温度为T₀的空气密封在两活塞之间，此时两活塞的位置如图所示。现对被密封的气体加热，使其温度缓慢上升到T。若活塞与圆筒壁之间的摩擦可忽略，此时两活塞之间气体的压强可能为多少？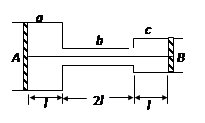

一定质量的理想气体，其状态变化图如右箭头顺序所示，AB平行于纵轴，BC平行于横轴，CA段是以纵轴和横轴为渐近线的双曲线的一部分，且已知A状态的压强和体积分别为P₀、V₀、T₀，且P_A＝3P_B，试求气体在B状态的温度和C状态的体积。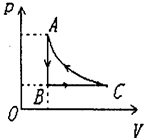  

如图所示，在一端封闭的U形管中用水银柱封一段空气柱L，当空气柱的温度为14℃时，左臂水银柱的长度h₁=10cm，右臂水银柱长度h₂=7cm，气柱长度L=15cm；将U形管放入100℃水中且状态稳定时，h₁变为7cm。分别写出空气柱在初末两个状态的气体参量，并求出末状态空气柱的压强和当时的大气压强（单位用cmHg）。

 如图，粗细均匀，内径很小，两端开口的U形管竖直放置。两管的竖直部分高度为20厘米，水平部分BC长16厘米。一空气柱把管内水银分成左右两部分。大气压强P₀=76cmHg，当空气柱温度为T₀=273K,长为L₀="10cm" 时，水平管BC内左边水银柱长为2 cm,，竖直管AB内水银柱长也为2cm .
求（1）空气柱右边水银柱总长是多少？
（2）当空气柱温度升高到多少时，左边水银恰好全部进入竖直管AB内？
（3）为使空气柱左侧管中水银全部溢出，空气柱温度至少要升高到多少？

如图示 ，光滑水平地面上放有一质量为m的导热气缸，用活塞封闭了一部分气体。活塞质量为m/2 ，截面积为S，可无摩擦滑动，气缸静止时与缸底距离为L₀。现用水平恒力F 向右推气缸，最后气缸与活塞达到相对静止状态。已知大气压强为P₀ .

求（1）稳定时封闭气体的压强
（2）稳定时活塞与缸底部的距离？