高中物理电荷守恒定律试题

如图所示：半径为R=1.8m的光滑圆轨道竖直固定在高h=5m的水平台上，平台BC长s=4.5m，一质量为m_b=1kg的小球b静止在C点。现让一质量为m_a=2kg的小球a从A点（与圆心等高）静止释放，运动到C点与b球发生碰撞，碰撞后a球的速度水平向右，a、b分别落在水平面上的M、N两点，M、N两点与平台的水平距离分别为x_a=3m、x_b=4m。两球可视为质点，g=10m/s²。求：

（1）碰撞后，b球获得的速度大小v_b；
（2）碰撞前，a球的速度大小v₀；
（3）判断BC段平台是否光滑？若不光滑，请求出平台的动摩擦因数。

有两滑块AB置于光滑的水平面上，A的质量为m，B的质量为2m，在水平面的右侧有一粗糙的斜面，斜面很长且倾角为，A、B两物体与斜面的动摩擦因素均为，且最大的静摩擦力等于滑动摩擦力。现突然给A施一水平向右冲量I，A、B碰撞无机械能损失，滑块由水平面运动至斜面也不考虑转弯处的机械能损失。求
1．A受冲量作用后的速度大小？
2．求AB碰后的速度?
3．若AB只发生一次碰撞，求摩擦力对B做功?

如图所示，水平面上放有一长为l的绝缘材料做成的滑板，滑板的右端有一固定竖直挡板。一质量为m、电荷量为+q的小物块放在滑板的左端。已知滑板的质量为8m，小物块与板面、滑板与水平面间的摩擦均不计，滑板和小物块均处于静止状态。某时刻使整个装置处于场强为E、方向水平向右的匀强电场中，小物块与挡板第一次碰撞后的速率为碰前的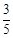。求：
（1）小物块与挡板第一次碰撞前瞬间的速率v₁；
（2）小物块与挡板第二次碰撞前瞬间的速率v₂；
（3）小物体从开始运动到第二次碰撞前，电场力做的功W。

如图所示，物体A、B的质量分别是m_A="4.0kg" ，m_B=6.0kg，用轻弹簧相连接放在光滑的水平面上，物体B左侧与竖直墙相接触．另有一个物体C以速度v₀=6.0m/s。向左运动，与物体A相碰，碰后立即与A粘在一起不再分开，然后以v’=2m/s的共同速度压缩弹簧，试求：

①物块C的质量m_C。
②在B离开墙壁之后，弹簧的最大弹性势能。

(9分)质量为2kg的平板车B上表面水平且车长为2．5m，原来静止在光滑水平面上，平板车一端静止着一块质量为2kg的物体A，一颗质量为0.01kg的子弹以700m／s的速度水平瞬间射穿A后，速度变为l00m／s，如果A与B之间的动摩擦因数为0.05，且子弹和物体A均可视为质点，重力加速度为g取10m／s²．求：

①A在平板车上运动的最大速度；
②A从B上滑离时，A和B的速度．

两根足够长的平行光滑导轨，相距1m水平放置。匀强磁场竖直向上穿过整个导轨所在的空间B =" 0.4" T。金属棒ab、cd质量分别为0.1kg和0.2kg，电阻分别为0.4Ω和0.2Ω，并排垂直横跨在导轨上。若两棒以相同的初速度3m/s向相反方向分开，不计导轨电阻，求：
①棒运动达到稳定后的ab棒的速度大小；
②金属棒运动达到稳定的过程中，回路上释放出的焦耳热；
③金属棒运动达到稳定后，两棒间距离增加多少？

12.如图所示,在光滑水平面上有两个并排放置的木块A和B,已知m_A="500" g,m_B="300" g,有一质量为80 g的小铜球C以25  m/s的水平初速开始,在A表面滑动,由于C和A,B间有摩擦,铜块C最后停在B上,B和C一起以2.5  m/s的速度共同前进,求:

(1)木块A的最后速度v_A′;
(2)C在离开A时速度v_C′.

如图所示，半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上，在桌面上轻
质弹簧被a、b两个小球挤压（小球与弹簧不拴接），处于静止状态。同时释放两个小球，
小球a、b与弹簧在桌面上分离后，a球从B点滑上光滑半圆环轨道最高点A时速度为
。已知小球a质量为m，小球b质量为2m，重力加速度为g。求：
（1）小球a在圆环轨道最高点对轨道的压力；
（2）释放后小球b离开弹簧时的速度的大小；
（3）释放小球前弹簧具有的弹性势能。

如图所示，光滑水平面上有一辆质量为Ｍ=1kg的小车，小车的上表面有一个质量为m=0.9kg的滑块，在滑块与小车的挡板间用轻弹簧相连接，滑块与小车上表面间的动摩擦因数为μ=0.2，整个系统一起以v₁=10m/s的速度向右做匀速直线运动，此时弹簧长度恰好为原长。现在用一质量为m₀=0.1kg的子弹，以v₀=50m/s的速度向左射入滑块且不穿出，所用时间极短。当弹簧压缩到最短时，弹簧被锁定，测得此时弹簧的压缩量为d=0.50m，g =10m/s²。求

①子弹射入滑块的瞬间，子弹与滑块的共同速度；
②弹簧压缩到最短时，弹簧弹性势能的大小。

如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为m_A、m_B、m_C，且；m_A=m_B =" 1.Okg" ,m_c = 2.O kg,其中B与C用一个轻弹簧拴接在一起，开始时整个装置处于静止状态.A和B之间有少许塑胶炸药，A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B，并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求：

(1) 塑胶炸药爆炸后瞬间A与B的速度各为多大？
(2) 在A追上B之前弹簧弹性势能的最大值；
(3) A与B相碰以后弹簧弹性势能的最大值.

（选修3-5）
（I）下列说法正确的是__________

A．放射性元素的半衰期是针对大量原子核的统计规律

B．α、β、γ射线比较，α射线的电离作用最弱

C．光的波长越短，光子的能量越大，光的粒子性越明显

D．核聚变原理是制造原子弹的理论基础

E．原子的全部正电荷和全部质量都集中在原子核里
F．由玻尔的原子模型可以推知，氢原子处于激发态，量子数越大，核外电子动能
越小
（II）如图所示，一轻质弹簧的一端固定在滑块B上，另一端与滑块C接触但未连接，该整体静置在光滑水平面上。现有一滑块A从光滑曲面上离水平面高处由静止开始滑下，与滑块B发生碰撞（时间极短）并粘在一起压缩弹簧推动滑块C向前运动，经过一段时间，滑块C脱离弹簧，继续在水平面上做匀速运动。已知,求：
（1）滑块A与滑块B碰撞时的速度大小；
（2）滑块A与滑块B碰撞结束瞬间它们的速度的大小；
（3）滑块C在水平面上匀速运动的速度的大小。

如图，倾角为θ的斜面固定。有n个质量都为m的相同的小木块（可视为质点）放置在斜面上。相邻两小木块间距离都为，最下端的木块距底端也是，小木块与斜面间的动摩擦因数都为μ。在开始时刻，第一个小木块从斜面顶端以初速度v₀沿斜面下滑，其余所有木块都静止，由于第一个木块的下滑将依次引起一系列的碰撞。设每次碰撞的时间极短，在每次碰撞后，发生碰撞的木块都粘在一起运动，直到最后第n个木块到达底端时，速度刚好为零。已知重力加速度为g．求：

第一次碰撞后小木块1的速度大小v；
从第一个小木块开始运动到第一次碰撞后系统损失的机械能；
发生一系列碰撞后，直到最后第n个木块到达底端，在整个过程中，由于碰撞所损失的总机械能_总。

如图所示，光滑水平面上静止放着长L=1.6m，质量为M=3kg的木块（厚度不计），一个质量为m=1kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ=0.1，今对木板施加一水平向右的拉力F，（g取10m/s²）

为使小物体不掉下去，F不能超过多少？
如果F=10N，求小物体所能获得的最大动能？
如果F=10N，要使小物体从木板上掉下去，F作用的时间不能小于多少？

如图所示，水平地面上静止放置着物块B和C，相距l=1.0m。物块A以速度v₀=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动，并再与C发生正碰，碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为，C的质量为A质量的K倍，物块与地面的动摩擦因数μ=0.45。（设碰撞时间很短，取10m/s²）

计算与C碰撞前瞬间AB的速度；
根据AB与C的碰撞过程分析K的取值范围，并讨论与C碰撞后AB的可能运动方向。

如图所示 ，粗糙斜面与光滑水平地面通过光滑小圆弧平滑连接，斜面倾角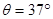，滑块A、C、D的质量均为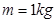，滑块B的质量为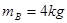，各滑块均可视为质点。A、B间夹着微量火药。K为处于原长的轻质弹簧，两端分别栓接滑块B和C。火药爆炸后，A与D相碰并粘在一起，沿斜面前进L =" 0.8" m 时速度减为零，接着使其保持静止。已知滑块A、D与斜面间的动摩擦因数均为 μ = 0.5，运动过程中弹簧始终处于弹性限度内，取 g = 10 m/s²，sin37°= 0.6，cos37°= 0.8。求：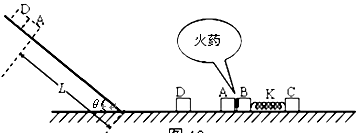

火药爆炸后A的最大速度v_A；
滑块B、C和弹簧K构成的系统在相互作用过程中，弹簧的最大弹性势能E_p；
滑块C运动的最大速度v_C。