高中物理电荷守恒定律计算题

如图所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R="0.45" m
的1/4圆弧面,A和D分别是圆弧的端点,BC段表面粗糙,其余段表面光滑,小滑块P₁和P₂的质量均为m,滑板的质量M=4m.P₁和P₂与BC面的动摩擦因数分别为μ₁=0.10和μ₂=0.40,最大静摩擦力近似等于滑动摩擦力,开始时滑板紧靠槽的左端,P₂静止在粗糙面的B点。P₁以v₀="4.0" m/s的初速度从A点沿弧面自由滑下,与P₂发生弹性碰撞后,P₁停在粗糙面B点上,当P₂滑到C点时,滑板恰好与槽的右端碰撞并与槽牢固粘连,P₂继续滑动,到达D点时速度为零,P₁与P₂可视为质点,取g="10" m/s²。问：

（1）P₂在BC段向右滑动时,滑板的加速度为多大？
（2）BC长度为多少？N、P₁和P₂最终静止后,P₁与P₂间的距离为多少？

如图所示，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰，碰后小球速度反向且动能是碰前动能的．已知木块与地面的动摩擦因素μ=，重力加速度取g．求：

（1）小球与木块碰前瞬间所受拉力大小
（2）木块在水平地面上滑行的距离

(1)研究发现两个氘核(H)可聚变成He，已知氘核的质量为2.013 6 u，中子的质量为1.008 7 u， He核质量为3.015 0 u．若质量亏损1 u对应的核能为931.5 MeV，则两个氘核聚变成He核的核反应方程为________________；上述反应中释放的核能为________．
(2)如图所示，光滑水平面上三个物块A、B、C，A、B间有压缩且被锁定的轻弹簧，三物块均处于静止状态．现解除对弹簧的锁定，B离开弹簧后，以速度v₀与C相碰，最终B与A运动的速度相同，已知m_A＝6 kg，m_B＝1 kg，m_C＝14 kg，求B与C相碰后C的速度大小．

(10分). “┙”型滑板，（平面部分足够长），质量为4m，距滑板的A壁为L₁距离的B处放有一质量为m，电量为+q的大小不计的小物体，小物体与板面的摩擦不计，整个装置处于场强为E的匀强电场中，初始时刻，滑板与小物体都静止，试求：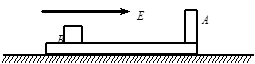

(1)释放小物体，第一次与滑板A壁碰前小物体的速度v₁多大？
(2)若小物体与A壁碰后相对水平面的速度大小为碰前的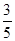，碰撞时间极短，则碰撞后滑板速度多大？（均指对地速度）
(3)若滑板足够长，小物体从开始运动到第二次碰撞前，电场力做功为多大？

(11分)光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板（平面部分足够长），滑板的质量为4m。距离滑板的右壁A为L₁的B处放有一质量为m、电量为+q(q>0)的小物体（可视为质点），小物体与板面之间的摩擦可忽略不计。整个装置处于场强为E、方向水平向右的匀强电场中。开始时，滑板与小物体都处于静止状态，某时刻释放小物体，求：

（1）小物体第一次跟滑板的A壁碰撞前瞬间的速度v₁多大;
（2）若小物体与A壁碰撞时间极短，且碰撞过程没有机械能损失，则
a.小物体第二次即将跟A壁碰撞瞬间，滑板的速度v和小物体的速度v₂分别为多大;
b.从开始释放小物体到它即将第二次跟A壁碰撞的过程中，整个装置的电势能减少了多少.

如图所示，光滑绝缘水平面的上方空间被竖直的分界面MN分隔成两部分，左侧空间有一水平向右的匀强电场，场强大小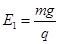，右侧空间有长为R＝0.114m的绝缘轻绳，绳的一端固定于O点，另一端拴一个质量为m小球B在竖直面内沿顺时针方向做圆周运动，运动到最低点时速度大小v_B＝10m/s（小球B在最低点时与地面接触但无弹力）。在MN左侧水平面上有一质量也为m，带电量为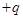的小球A，某时刻在距MN平面L位置由静止释放，恰能与运动到最低点的B球发生正碰，并瞬间粘合成一个整体C。（取g＝10m/s²）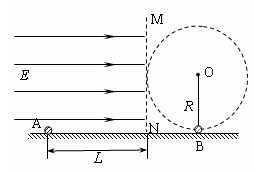

（1）如果L＝0.2m，求整体C运动到最高点时的速率。（结果保留1位小数）
（2）在（1）条件下，整体C在最高点时受到细绳的拉力是小球B重力的多少倍？（结果取整数）
（3）若碰后瞬间在MN的右侧空间立即加上一水平向左的匀强电场，场强大小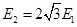，当L满足什么条件时，整体C可在竖直面内做完整的圆周运动。（结果保留1位小数）

如图所示，固定在水平地面上的横截面为“”形的光滑长直导轨槽，槽口向上（图为俯视图,图中两组平行双直线表示“”形槽的两侧壁）．槽内放置一个滑块，滑块的左半部是半径为R的半圆柱形光滑凹槽，滑块的宽度为2R，恰与“”形槽的两内侧壁的间距相等，滑块可在槽内沿槽壁自由滑动．现有一金属小球（可视为质点）以水平初速度v₀沿槽的一侧壁冲向滑块，从滑块的半圆形槽口边缘进入滑块凹槽．已知金属小球的质量为m，滑块的质量为3m，整个运动过程中无机械能损失．求：

（1）当金属小球滑离滑块时，金属小球和滑块的速度各是多大；
（2）当金属小球经过滑块上的半圆柱形槽的最右端A点时，金属小球的对地速率．

(18分)如图所示，质量M=4kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质 弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，可视为质点的小木块A质量m=1kg，原来静止于滑板的左端，滑板与木块A之间的动摩擦因数μ=0.2．当滑板B受水平向左恒力F=14N作用时间t后，撤去F，这时木块A恰好到达弹簧自由端C处，此后运动过程中弹簧的最大压缩量为s=5cm．g取10m/s²．  
求：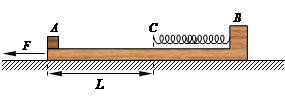

（1）水平恒力F的作用时间t；
（2）木块A压缩弹簧过程中弹簧的最大弹性势能；
（3）当小木块A脱离弹簧且系统达到稳定后，整个运动过程中系统所产生的热量．

(10分)如图所示，在光滑水平地面上，有一质量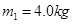的平板小车，小车的右端有一固定的竖直挡板，挡板上固定一轻质细弹簧．位于小车上A点处的质量为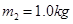的木块(视为质点)与弹簧的左端相接触但不连接，此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间有摩擦，与A点右侧的车面之间的摩擦可忽略不计．现小车与木块一起以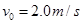的初速度向右运动，小车将与其右侧的竖直墙壁发生碰撞，已知碰撞时间极短，碰撞后小车以的速度水平向左运动，取．

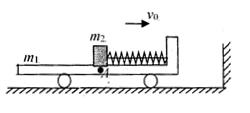
(i)求小车与竖直墙壁发生碰撞的过程中小车动量变化量的大小；
(ii)若弹簧始终处于弹性限度内，求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能；

一质量为电荷量的与外界绝缘物块A（可视为质点），置于光滑水平面上。A与弹簧左端相连接，弹簧右端固定在竖直墙面上，整个空间中存在水平向右的匀强电场，场强，平衡时弹簧的压缩量为.如图O为弹簧原长时的位置，另一个质量也为电量为的绝缘带电物块B（可视为质点），从O点左侧距离O为处的P点由静止释放，当它打在A物块上时立即与A一起向右运动，但不粘连，它们到达最右端后又向左运动，试求：物块B向左运动达到最远点时距O点的距离？（AB相撞在瞬间完成，电荷无转移，不计AB间库仑力，弹簧始终在弹性限度内）。

如图所示，长S＝10m的平台AB固定，长L=6m质量M=3kg的木板放在光滑地面上，与平台平齐且靠在B处，右侧有落差h=0.1m的光滑弧形桥CD（桥的支柱未画出），桥面的最低位置与AB水平线等高（木板可从桥下无障碍的前行）。已知木板右侧与弧形桥左侧C端的水平距离d=1.5m，弧形桥顶部圆弧半径相等R=0.4m（半径未画出）。现有质量m=1kg的物块，以初速度v₀=12m/s从A点向右运动，过B点后滑上木板，物块与平台、木板间的滑动摩擦因数 μ＝0.4，物块滑上弧形桥时无机械能损失，当物块到达圆弧最高点时D时，木板中点刚好到达D点正下方。物块大小忽略，重力加速度g=10m/s²。求：

（1）物块滑至B点时的速度大小v；
（2）物块与木板能否达到共速，若能，确定两物体共速时木板的位置和物块在木板上的位置；
（3）物块到达弧形桥顶端D点时所受到的支持力F及物块与木板相碰点到木板左端的距离S₀.

如图，绝缘水平地面上有宽L=0.4m的匀强电场区域，场强，方向水平向左。带电的物块B静止在电场边缘的O点，带电量、质量的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍，A、B与地面间的动摩擦因数都为=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/_S²。

(1) 求A到达O点与B碰撞前的速度大小；
(2) 求碰撞后瞬间A和B的速度大小；
(3) 讨论K在不同取值范围时电场力对A做的功。

如图，在倾角为的足够长的光滑绝缘斜面上，带正电的物块A和不带电绝缘物块B相距.，物块A位于斜面底端，斜面处于范围足够大、方向平行斜面向上的匀强电场中。将A、B同时由静止释放，两物块恰好在AB中点处发生第一次碰撞， A、B碰撞过程相互作用时间极短，已知A、B碰撞过程无机械能损失，且A的电荷没有转移，A、B均可视为质点，重力加速度为。求： 

（1）第一次相碰前瞬间A、B的速度大小；
（2）第一次碰撞后，第二次碰撞前，A、B之间的最大距离； 
（3）若斜面长度有限，要使A、B仅能在斜面上发生两次碰撞，试求斜面长度的范围。

如图所示，光滑固定轨道的两端都是半径为R的四分之一圆弧，在轨道水平面上有两个质量均为m的小球B、C，B、C用一长度锁定不变的轻小弹簧栓接，弹性势能．一质量也为m的小球A从左侧的最高点自由滑下，A滑到水平面与B碰后立即粘在一起结合成D就不再分离（碰撞时间极短）．当D、C一起刚要滑到右侧最低点时，弹簧锁定解除且立即将C弹出并与弹簧分离．求

（1）弹簧锁定解除前瞬间，D、C速度大小
（2）弹簧锁定解除后，C第一次滑上轨道右侧圆弧部分的轨迹所对的圆心角
（3）弹簧锁定解除后，若C、D（含弹簧）每次碰撞均在水平面；求第N次碰撞结束时，C、D的速度

如图所示，长木板A上右端有一物块B，它们一起在光滑的水平面上向左做匀速运动，速度v₀=2m/s。木板左侧有一个与木板A等高的固定物体C。已知长木板A的质量为m_A=1.0kg，物块B的质量为m_B=3.0kg，物块B与木板A间的动摩擦因数μ=0.5，取g=10m/s²。

（1）若木板A足够长，A与C第一次碰撞后，A立即与C粘在一起，求物块 B在木板A上滑行的距离L应是多少；
（2）若木板足够长，A与C发生碰撞后弹回（碰撞时间极短，没有机械能损失），求第一次碰撞后A、B具有共同运动的速度v；
（3）若木板A长为0.48m，且A与C每次碰撞均无机械能损失，求A与C碰撞几次，B可脱离A？