高中物理电荷守恒定律计算题

如图所示，一质量M=2kg的带有弧形轨道的平台置于足够长的水平轨道上，弧形轨道与水平轨道平滑连接，水平轨道上静置一小球B。从弧形轨道上距离水平轨道高h=0.3m处由静止释放一质量m_A=1kg的小球A，小球A沿轨道下滑后与小球B发生弹性正碰，碰后小球A被弹回，且恰好追不上平台。已知所有接触面均光滑，重力加速度为g。求小球B的质量。

如图所示，有一内表面光滑的金属盒，底面长为L=1.2m，质量为m₁=1kg，放在水平面上，与水平面间的动摩擦因数为μ=0.2，在盒内最右端放一半径为r=0.1m的光滑金属球，质量为m₂=1kg，现在盒的左端，给盒一个初速度v=3m/s（盒壁厚度，球与盒发生碰撞的时间和能量损失均忽略不计，g取10m/s²）求：金属盒从开始运动到最后静止所经历的时间?

如图甲所示，物块A、B的质量分别是 ="4.0" kg和="3.0" kg。用轻弹簧拴接，放在光滑的水平地面上，物块B右侧与竖直墙相接触。另有一物块C从t=0时以一定速度向右运动，在t="4" s时与物块A相碰，并立即与A粘在一起不再分开，物块C的v-t图像如图乙所示。求：

①物块C的质量 ？
②B离开墙后的运动过程中弹簧具有的最大弹性势能？

如图所示，在光滑的水平面上，质量为4m、长为L的木板右端紧靠竖直墙壁，与墙壁不粘连。质量为m的小滑块（可视为质点）以水平速度v₀滑上木板左端，滑到木板右端时速度恰好为零。现小滑块以水平速度v滑上木板左端，滑到木板右端时与竖直墙壁发生弹性碰撞，以原速率弹回，刚好能够滑到木板左端而不从木板上落下，求的值。

用轻质弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑的水平地面上运动，弹簧处于原长，质量为4kg的物块C静止于前方，如图所示，B与C碰撞后二者粘在一起运动，求：

①当弹簧的弹性势能最大时，物块A的速度多大?
②弹簧弹性势能的最大值是多少?

如图所示，在光滑水平面上放着一个质量M＝0．3kg的木块（可视为质点），在木块正上方1m处有一个固定悬定点O，在悬点O和木块之间用一根长2m、不可伸长的轻绳连接。有一颗质量m＝0．1kg的子弹以80m/s的速度水平射入木块并留在其中，之后木块绕O点在竖直平面内做圆周运动。求：

①木块以多大速度脱离水平地面?
②当木块到达最高点时对轻绳的拉力F为多少?

质量为M=2kg的木块固定在光滑的水平地面上，质量为m=0.04kg的子弹以速度v₁=500m/s射入．射出时速度为v₂=300m/s．如图所示，今将钉子拔掉，子弹射出后速度多大？

卢瑟福用α粒子轰击氮核发现质子。发现质子的核反应为：。已知氮核质量为m_N=14.00753u，氧核的质量为m_O=17.00454u，氦核质量m_He=4.00387u，质子（氢核）质量为m_p=1.00815u。（已知：1uc²=931MeV，结果保留2位有效数字）求：
（1）这一核反应是吸收能量还是放出能量的反应？相应的能量变化为多少？
（2）若入射氦核以v₀=3×10⁷m/s的速度沿两核中心连线方向轰击静止氮核。反应生成的氧核和质子同方向运动，且速度大小之比为1:50。求氧核的速度大小。

）（如图，总质量为M=100kg的人和箱子，一起以v₀=10m/s的速度在光滑水平的冰面上匀速滑行，前进中突然发现前方有一矮墙。为避免撞墙，人将质量m=40kg的箱子水平推向墙，箱子撞墙后以原速率反向弹回，之后人又接住箱子。求人推出箱子的速度至少多大才能在完成一次推接后避免撞墙。

）（在足够长的水平光滑直导轨上，静止放着三个质量均为m＝1 kg的相同小球A、B、C，现让A球以v₀＝2 m/s的速度正对着B球运动，A、B两球碰撞后粘在一起，两球继续向右运动并与C球发生正碰，C球的最终速度v_C＝1 m/s。求：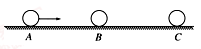

（1）A、B两球与C球相碰前的共同速度多大？
（2）两次碰撞过程中一共损失了多少动能？

如图所示，光滑平台上有两个刚性小球A和B，质量分别为2m和3m，小球A以速度v₀向右运动并与静止的小球B发生碰撞（碰撞过程不损失机械能），小球B飞出平台后经时间t刚好掉入装有沙子向左运动的小车中，小车与沙子的总质量为m，速度为2v₀，小车行驶的路面近似看做是光滑的，求：

（1）碰撞后小球A和小球B的速度；
（2）小球B掉入小车后的速度。

如右图所示，光滑的水平面AB与半径为R="0.32" m的光滑竖直半圆轨道BCD在B点相切，D为轨道最高点．用轻质细线连接甲、乙两小球，中间夹一轻质弹簧，弹簧与甲、乙两球不拴接．甲球的质量为m₁="0.1" kg，乙球的质量为m₂="0.3" kg，甲、乙两球静止在光滑的水平面上。现固定甲球，烧断细线，乙球离开弹簧后进入半圆轨道恰好能通过D点。重力加速度g取10 m/s²，甲、乙两球可看作质点。

①试求细线烧断前弹簧的弹性势能；
②若甲球不固定，烧断细线，求乙球离开弹簧后进入半圆轨道能达到的最大高度；

如图所示，小球A以速率v₀向右运动时跟静止的小球B发生碰撞，碰后A球以的速率弹回，而B球以的速率向右运动，求A、B两球的质量之比。

如图所示，一质量为3 kg的平板车M放在光滑水平面上，在其右端放一质量为2 kg的小木块m，木块与平板车间动摩擦因数为μ＝0.5，现给木块和平板车以大小相等、方向相反的初速度v₀＝3 m/s，（g取10 m/s²）求：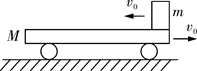

（1）运动过程中小木块不滑出平板车，平板车至少多长；
（2）从地面上看，小木块向左运动到离出发点最远处时，平板车向右运动位移大小．

）（一轻质弹簧竖直固定在地面上，上面连接一个质量为m₁=1kg的物体，平衡时物体离地面0.9m，弹簧所具有的弹性势能为0.5J。现在在距物体m₁正上方高为0.3m处有一个质量为m₂=1kg的物体自由下落后与弹簧上物体m₁碰撞立即合为一体，一起向下压缩弹簧。当弹簧压缩量最大时，弹簧长为0.6m。求（g取10m/s²）：

①碰撞结束瞬间两物体的动能之和是多少？
②弹簧长为0.6m时弹簧的弹性势能大小？