高中物理等势面计算题

如图所示，在两条平行的虚线内存在着宽度为L、电场强度为E的匀强电场，在与右侧虚线相距也为L处有一与电场平行的屏．现有一电荷量为＋q、质量为m的带电粒子(重力不计)，以垂直于电场线方向的初速度v₀射入电场中，v₀方向的延长线与屏的交点为O.试求：

(1)粒子从射入到打到屏上所用的时间；
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tan α；
(3)粒子打到屏上的点P到O点的距离x.

水平放置的平行金属板AB间的距离d=0.1m，板长L=0.3m，在金属板的左端竖直放置一带有小孔的挡板，小孔恰好位于AB板的正中间，距金属板右端x=0.5m处竖直放置一足够大的荧光屏，现在AB板间加如图（b）所示的方波形电压，已知U₀=1.0×10²V，在挡板的左侧，有大量带正电的相同粒子以平行于金属板方向的速度持续射向挡板，粒子的质量m=1.0×10^-7kg，电荷量q=1.0×10^-2C，速度大小均为v₀=1.0×10⁴m/s，带电粒子的重力不计，则：

（1）求粒子在电场中的运动时间；
（2）求在t=0时刻进入的粒子打在荧光屏上的位置到O点的距离；
（3）请证明粒子离开电场时的速度均相同；
（4）若撤去挡板，求荧光屏上出现的光带长度。

(15分)某一水平面内有一直角坐标系平面，和的区间内有一沿轴负方向的有理想边界的匀强电场，场强大小为；在和的区间内有一沿轴负方向的有理想边界的匀强电场场强大小为且一比荷为带负电粒子从直角坐标系平面内的坐标原点以很小的速度进入匀强电场，计算时不计此速度和粒子自身的重力，且只考虑粒子在平面内的运动。试求：

（1）粒子从O点进入到离开处的电场所需的时间；
（2）电子离开处的电场时的坐标；
（3）电子离开处的电场时的速度大小和方向。

如图所示，绝缘倾斜固定轨道上A点处有一带负电，电量大小q=0.4C质量为0.3kg的小物体，斜面下端B点有一小圆弧刚好与一水平放置的薄板相接，AB点之间的距离S=1.92m，斜面与水平面夹角θ=37°，物体与倾斜轨道部分摩擦因数为0.2，斜面空间内有水平向左，大小为E₁=10V/m的匀强电场，现让小物块从A点由静止释放，到达B点后冲上薄板，薄板由新型材料制成，质量M=0.6kg，长度为L，物体与薄板的动摩擦因数μ=0.4，放置在高H="1." 6m的光滑平台上，此时，在平台上方虚线空间BCIJ内加上水平向右，大小为E₂=1.5V/m的匀强电场，经t=0.5s后，改成另一水平方向的电场E₃，在此过程中，薄板一直加速，到达平台右端C点时，物体刚好滑到薄板右端，且与薄板共速，由于C点有一固定障碍物，使薄板立即停止，而小物体则以此速度V水平飞出，恰好能从高h=0.8m的固定斜面顶端D点沿倾角为53°的斜面无碰撞地下滑，（重力加速度g=10m/s²，sin37°=，cos37°=）求：

（1）小物体水平飞出的速度v及斜面距平台的距离x；
（2）小物体运动到B点时的速度v_B；
（3）电场E₃的大小和方向，及薄板的长度L。

“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成．偏转器是由两个相互绝缘、半径分别为R_A和R_B的同心金属半球面A和B构成，A、B为电势值不等的等势面，其过球心的截面如图所示．一束电荷量为E、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射，进入偏转电场区域，最后到达偏转器右端的探测板N，其中动能为E_k0的电子沿等势面C做匀速圆周运动到达N板的正中间．忽略电场的边缘效应．

（1）判断球面A、B的电势高低，并说明理由；
（2）求等势面C所在处电场强度E的大小；
（3）若半球面A、B和等势面C的电势分别为φ_A、φ_B和φ_C，则到达N板左、右边缘处的电子，经过偏转电场前、后的动能改变量△E_k左和△E_k右分别为多少？
（4）比较|△E_k左|和|△E_k右|的大小，并说明理由．

“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成．偏转器是由两个相互绝缘、半径分别为R_A和R_B的同心金属半球面A和B构成，A、B为电势值不等的等势面，其过球心的截面如图所示．一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射，进入偏转电场区域，最后到达偏转器右端的探测板N，其中动能为E_k0的电子沿等势面C做匀速圆周运动到达N板的正中间．忽略电场的边缘效应．

（1）判断球面A、B的电势高低，并说明理由；
（2）求等势面C所在处电场强度E的大小；
（3）若半球面A、B和等势面C的电势分别为φ_A、φ_B和φ_C，则到达N板左、右边缘处的电子，经过偏转电场前、后的动能改变量△E_k左和△E_k右分别为多少？
（4）比较|△E_k左|和|△E_k右|的大小，并说明理由．

（1）如图1所示，固定于水平面上的金属框架abcd，处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行，bc与ab、dc垂直。MN与bc的长度均为l，在运动过程中MN始终与bc平行，且与框架保持良好接触。磁场的磁感应强度为B。

a. 请根据法拉第电磁感应定律，推导金属棒MN中的感应电动势E；
b. 在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E。
（2）为进一步研究导线做切割磁感线运动产生感应电动势的过程，现构建如下情景：如图2所示，在垂直于纸面向里的匀强磁场中，一内壁光滑长为l的绝缘细管MN，沿纸面以速度v向右做匀速运动。在管的N端固定一个电量为q的带正电小球（可看做质点）。某时刻将小球释放，小球将会沿管运动。已知磁感应强度大小为B，小球的重力可忽略。在小球沿管从N运动到M的过程中，求小球所受各力分别对小球做的功。

在光滑绝缘的水平面上,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的带电荷量为+2q,b球的带电荷量为-3q,组成一带电系统,如图所示,虚线MP为AB两球连线的垂直平分线,虚线 NQ与MP平行且相距4L.最初A和B分别静止于虚线MP的两侧,距MP的距离均为L,且A球距虚线 NQ的距离为3L.若视小球为质点,不计轻杆的质量,在虚线MP､ NQ间加上水平向右的匀强电场E后,求: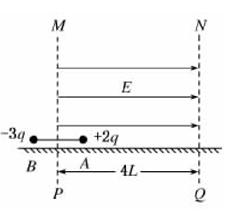

(1) B球刚进入电场时,带电系统的速度大小.
(2)带电系统从开始运动到速度第一次为零所需时间以及B球电势能的变化量.