
(1)磁感应强度B的大小;
(2)在0~0.5s时间内金属棒的加速度a的大小;
(3)若在0~0.3s时间内电阻R产生的热量为0.15J,则在这段时间内电动机做的功。

(1)该粒子的比荷(q/m)
(2)若偏转磁场为半径为 的圆形区域,且与MN相切于G点,如图乙所示,其它条件不变.仍保证上述粒子从G点垂直于MN进入偏转磁场,最终仍然到达照相底片上的H点,则磁感应强度
的圆形区域,且与MN相切于G点,如图乙所示,其它条件不变.仍保证上述粒子从G点垂直于MN进入偏转磁场,最终仍然到达照相底片上的H点,则磁感应强度 的比值为多少?
的比值为多少?
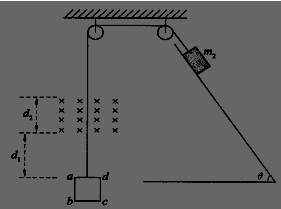
(1)线框ad边从磁场上边缘穿出时绳中拉力的功率;
(2)线框刚刚全部进入磁场时速度的大小;
(3)整个运动过程中线框产生的焦耳热。
|
如图甲所示,两根足够长的竖直光滑平行金属导轨相距为L1=0.1m,导轨下端通过导线连接阻值R=0.4Ω的电阻。质量为m=0.2kg、阻值r=0.1Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处于垂直导轨平面向外的磁场中,取g=10m/s2.
(1)若金属棒距导轨下端L2=0.2m,磁场随时间变化的规律如图乙所示,为保持金属棒静止,试求加在金属棒中央、沿竖直方向的外力随时间变化的关系;
(2)若所加磁场的磁感应强度大小恒为 ,通过恒定功率Pm=6W的竖直向上的拉力使棒从静止开始向上运动,其棒向上运动的位移随时间变化的情况如图丙所示,试求磁感应强度
,通过恒定功率Pm=6W的竖直向上的拉力使棒从静止开始向上运动,其棒向上运动的位移随时间变化的情况如图丙所示,试求磁感应强度 的大小和变速运动阶段在电阻R上产生的热量。
的大小和变速运动阶段在电阻R上产生的热量。
如图所示,电子源每秒钟发射2.50×1013个电子,以v0=8.00×106m/s的速度穿过P板上的A孔,从M、N两平行板正中央进入两板间,速度方向平行于板M且垂直于两板间的匀强磁场,板M、N两板间电压始终为UMN="80.O" V,两板距离为d=1.00×10-3m,电子在板M、N间做匀速直线运动后进入由C、D两平行板组成的已充电的电容器中,电容器电容为8.00×10-8F,电子打到D板后就留在D板中,在时刻tl=0,D板电势较C板高818V,在时刻t2=T,开始有电子打到M板上,已知电子质量m=9.10×10-31kg,电量e=1.60×10-19C,电子从A孔到D板的运动时间不计,C、P两板均接地,电子间不会发生碰撞。求:
(1)M、N间匀强磁场的磁感应强度大小。
(2)时间T及打到M板上的每个电子的动能(以eV为单位)。
在如图甲所示的电路中,螺线管匝数n = 1500匝,横截面积S = 20cm2。螺线管导线电阻r = 1.0Ω,R1 = 4.0Ω,R2 = 5.0Ω,C=30μF。在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化。求:
(1)求螺线管中产生的感应电动势;
(2)闭合S,电路中的电流稳定后,求电阻R1的电功率;
(3)S断开后,求流经R2的电量。
人们到医院检查身体时,其中有一项就是做胸透,我们可以把做胸透的原理等效如下:如图所示,P是一个放射源,从开口处在纸面内向各个方向放出某种粒子(不计重力),而这些粒子最终必须全部垂直射到底片MN这一有效区域,并要求底片MN上每一地方都有粒子到达。假若放射源所放出的是质量为m、电量为q的带正电的粒子,且所有的粒子速率都是v,M与放射源的出口在同一水平面,底片MN竖直放置,底片MN长为L。
为了实现上述目的,我们必须在P的出口处放置一有界匀强磁场。求:
(1)匀强磁场的方向
(2)画出所需最小有界匀强磁场的区域,并用阴影表示
(3)匀强磁场的磁感应强度B的大小以及最小有界匀强磁场的面积S
如图所示,直角坐标系 所决定的平面内,在平行于y轴的虚线MN右侧、y>0的区域存在着沿y轴负方向的匀强电场;在y<0的某 区域存在方向垂直于坐标平面的圆形有界匀强磁场(图中未画出)。现有一电荷量为
所决定的平面内,在平行于y轴的虚线MN右侧、y>0的区域存在着沿y轴负方向的匀强电场;在y<0的某 区域存在方向垂直于坐标平面的圆形有界匀强磁场(图中未画出)。现有一电荷量为 、质量为
、质量为 的带正电粒子从虚线MN上的P处,以平行于
的带正电粒子从虚线MN上的P处,以平行于 轴方向的初速度
轴方向的初速度 射人电场,并恰好从原点
射人电场,并恰好从原点 处射出,射出时速度方向与
处射出,射出时速度方向与 轴成60°角,此后粒子先做匀速运动,然后进入磁场。粒子从圆形有界磁场中射出时,恰好位于y轴上Q(0,一
轴成60°角,此后粒子先做匀速运动,然后进入磁场。粒子从圆形有界磁场中射出时,恰好位于y轴上Q(0,一 )处,且射出时速度方向沿
)处,且射出时速度方向沿 轴负方向,不计带电粒子的重力。求:
轴负方向,不计带电粒子的重力。求:
(1) 两点间的电势差。
两点间的电势差。
(2)匀强磁场的磁感应强度。
(3)圆形有界匀强磁场的最小面积。
(结果用 表示)
表示) 
试题篮
()