如图所示是粒子速度选择器的原理图,如果粒子所具有的速率 ,那么
,那么
| A.带正电粒子必须沿虚线方向从左侧进入场区,才能沿直线通过 |
| B.带负电粒子必须沿虚线方向从右侧进入场区,才能沿直线通过 |
| C.不论粒子电性如何,沿虚线方向从左侧进入场区,都能沿直线通过 |
| D.不论粒子电性如何,沿虚线方向从右侧进入场区,都不能沿直线通过 |
有关电场力和洛伦兹力,以下说法正确的是
| A.在电场中,电荷无论运动还是静止一定会受到电场力的作用 |
| B.在磁场中,只有电荷运动一定会受到洛伦兹力的作用 |
| C.电荷在电场中运动,电场力对电荷一定做功 |
| D.电荷在磁场中运动,洛伦兹力对电荷一定不做功 |
如图甲,真空中竖直放置两块相距为d的平行金属板P、Q,两板间加上如图乙最大值为U0的周期性变化的电压,在Q板右侧某个区域内存在磁感应强度大小为B、方向垂直于纸面向里的有界匀强磁场。在紧靠P板处有一粒子源A,自t=0开始连续释放初速不计的粒子,经一段时间从Q板小孔O射入磁场,然后射出磁场,射出时所有粒子的速度方向均竖直向上。已知电场变化周期 ,粒子质量为m,电荷量为+q,不计粒子重力及相互间的作用力。求:
,粒子质量为m,电荷量为+q,不计粒子重力及相互间的作用力。求:
(1)t=0时刻释放的粒子在P、Q间运动的时间;
(2)粒子射入磁场时的最大速率和最小速率;
(3)有界磁场区域的最小面积。
如图所示的平面直角坐标系 ,在第一象限内有平行于
,在第一象限内有平行于 轴的匀强电场,方向沿
轴的匀强电场,方向沿 轴负方向;在第四象限的正方形
轴负方向;在第四象限的正方形 区域内有匀强磁场,方向垂直于
区域内有匀强磁场,方向垂直于 平面向外,正方形边长为L,且
平面向外,正方形边长为L,且 边与
边与 轴平行。一质量为
轴平行。一质量为 、电荷量为
、电荷量为 的粒子,从
的粒子,从 轴上的
轴上的 点,以大小为
点,以大小为 的速度沿
的速度沿 轴正方向射入电场,通过电场后从
轴正方向射入电场,通过电场后从 轴上的
轴上的 点进入磁场,最后从
点进入磁场,最后从 点离开磁场,且速度方向与
点离开磁场,且速度方向与 边成
边成 角,不计粒子所受的重力,求:
角,不计粒子所受的重力,求:
(1)判断粒子带电的电性,并求电场强度E的大小;
(2)粒子到达 点时速度
点时速度 的大小和方向;
的大小和方向;
(3)求 区域内磁场的磁感应强度B。
区域内磁场的磁感应强度B。
如图所示,在y轴右侧有一方向垂直纸面向里的有界匀强磁场区域(图中未画出),磁感应强度大小为B。一束质量为m电量为+q的粒子流,沿x轴正向运动,其速度大小介于v0与2v0之间,从坐标原点射入磁场,经磁场偏转后,所有粒子均沿y轴正方向射出磁场区域。不计粒子重力。
求
(1)粒子在磁场中运动的最大半径和最小半径。
(2)粒子在磁场中运动的时间。
(3)满足条件的磁场区域的最小面积。
如图所示,一带电小球质量为m,用丝线悬挂于O点,并在竖直平面内摆动,最大摆角为60°,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,则小球自右方摆到最低点时悬线上的张力为( )

| A.0 | B.2mg | C.4mg | D.6mg |
在平面直角坐标系xOy中,第I象限存在沿y轴负方向的匀强电场,第IV象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m,电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求
(1)M、N两点间的电势差UMN;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t.
一个质量 的小滑块,带有
的小滑块,带有 的电荷放置在倾角
的电荷放置在倾角 的光滑斜面上(绝缘),斜面置于
的光滑斜面上(绝缘),斜面置于 的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面滑下,其斜面足够长,小滑块滑至某一位置时,要离开斜面(
的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面滑下,其斜面足够长,小滑块滑至某一位置时,要离开斜面( )。求:
)。求:
(1)小滑块带何种电荷?
(2)小滑块离开斜面的瞬时速度多大?
(3)该斜面的长度至少多长?
目前世界上正研究的一种新型发电机叫磁流体发电机,如图表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体来说(呈中性)沿图中所示方向喷射入磁场,磁场中有两块金属板A、B,这时金属板上就聚集了电荷.在磁极配置如图所示的情况下,下述说法正确的是( )


A.A板带正电
B.有电流从b经用电器流向a
C.金属板A、B间的电场方向向下
D.等离子体发生偏转的原因是离子所受洛伦兹力大于所受电场力
如图所示,在xoy坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场的磁感应强度大小为B,方向垂直于纸面向里。在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E。从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r。已知质子的电荷量为q,质量为m,不计质子所受重力及质子间相互作用力的影响。
(1)求质子射入磁场时速度的大小;
(2)若质子沿x轴正方向射入磁场,求质子从O点进入磁场到第二次离开磁场经历的时间;
(3)若质子沿与x轴正方向成夹角θ的方向从O点射入第一象限的磁场中,求质子在磁场中运动的总时间。
如图所示的圆形区域内有匀强磁场,其边界跟y轴在坐标原点O处相切;磁感应强度为B,方向垂直于纸面向里,在O处有一放射源可沿纸面向各个方向射出速率均为v的带电粒子;已知带电粒子质量为m,电荷量q,圆形磁场区域的半径 ,则粒子在磁场中运动的最长时间是多少?
,则粒子在磁场中运动的最长时间是多少?

如图所示,在平面直角坐标系xoy内,第一象限存在沿y轴负方向的匀强电场,一质量为m,电荷量为q的带正电的粒子,从y轴正半轴上y=d处的M点,以速度v0垂直于y轴射入电场,经x轴上 处的N点进入第四象限,在第四象限适当区域内存在方向垂直于纸面向外的匀强磁场,磁感应强度为B,已知此磁场仅分布在一个圆形区域内(图中未画出),粒子进入磁场后,最后以垂直于y轴的方向射出磁场,不计粒子重力。求:
处的N点进入第四象限,在第四象限适当区域内存在方向垂直于纸面向外的匀强磁场,磁感应强度为B,已知此磁场仅分布在一个圆形区域内(图中未画出),粒子进入磁场后,最后以垂直于y轴的方向射出磁场,不计粒子重力。求:
(1)电场强度的大小E;
(2)粒子在N点时的速度大小和方向;
(3)粒子在磁场中运动时间;
(4)圆形区域的最小面积。
汤姆孙提出的测定带电粒子的比荷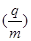 的实验原理如图所示。带电粒子经过电压为U的加速电场加速后,垂直于磁场方向进入宽为L的有界匀强磁场,带电粒子穿过磁场时发生的偏转位移是d,若磁场的磁感应强度为B。则带电粒子的比荷为
的实验原理如图所示。带电粒子经过电压为U的加速电场加速后,垂直于磁场方向进入宽为L的有界匀强磁场,带电粒子穿过磁场时发生的偏转位移是d,若磁场的磁感应强度为B。则带电粒子的比荷为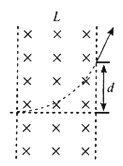
A.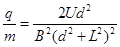
B.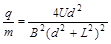
C.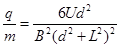
D.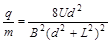
试题篮
()