一个带电粒子,沿垂直于磁场方向,射入匀强磁场中,粒子的一段径迹如图所示,径迹上的每一小段都可以近似看成圆弧.由于带电粒子使周围的空气电离,粒子的能量逐渐减小而带电量不变.不计粒子重力,从图中情况可以确定( )

| A.粒子是带正电的,它所受的洛仑兹力大小不变 |
| B.粒子是带正电的,它是由a点运动到b点 |
| C.粒子是带负电的,它所受的洛仑兹力大小逐渐增大 |
| D.粒子是带负电的,它是由a点运动到b点 |
如图所示,半径为r的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上A点有一离子源,能平行于纸面源源不断地向各种方向发射速度大小均为2kBr的带正电的粒子(重力不计),其中k为粒子的比荷,则粒子在磁场中运动的最长时间为
A. |
B. |
C. |
D. |
如图所示,有界匀强磁场的磁感应强度为B,宽度为d,一电子从磁场做边界垂直射入,当其从右边界穿出时速度方向与入射方向的夹角为30°,已知的质量m,电量为e,不计电子的重力,求:
(1)电子的在磁场中的运动的半径;
(2)电子入射速度的大小;
(3)电子穿过磁场的时间。
质谱仪是测量带电粒子的质量和分析同位素的重要工具,如图为质谱仪原理示意图,现利用这种质谱仪对氢元素进行测量,氢元素的各种同位素从容器A下方的小孔S无初速度飘入电压为U的加速电场,加速后垂直进入磁感应强度为B的匀强磁场中,氢的三种同位素氕氘氚的电量之比为1:1:1,质量之比为1:2:3,它们最后打在照相底片D上,形成a、b、c三条质谱线,下列判断正确的是
| A.进入磁场时速度从大到小排列的顺序是氚、氘、氕 |
| B.进入磁场时速度从大到小排列的顺序是氕、氘、氚 |
| C.a、b、c三条质谱线依次排列的顺序为氚、氘、氕 |
| D.a、b、c三条质谱线依次排列的顺序为氕、氘、氚 |
如图所示是粒子速度选择器的原理图,如果粒子所具有的速率 ,那么
,那么
| A.带正电粒子必须沿虚线方向从左侧进入场区,才能沿直线通过 |
| B.带负电粒子必须沿虚线方向从右侧进入场区,才能沿直线通过 |
| C.不论粒子电性如何,沿虚线方向从左侧进入场区,都能沿直线通过 |
| D.不论粒子电性如何,沿虚线方向从右侧进入场区,都不能沿直线通过 |
有关电场力和洛伦兹力,以下说法正确的是
| A.在电场中,电荷无论运动还是静止一定会受到电场力的作用 |
| B.在磁场中,只有电荷运动一定会受到洛伦兹力的作用 |
| C.电荷在电场中运动,电场力对电荷一定做功 |
| D.电荷在磁场中运动,洛伦兹力对电荷一定不做功 |
如图甲,真空中竖直放置两块相距为d的平行金属板P、Q,两板间加上如图乙最大值为U0的周期性变化的电压,在Q板右侧某个区域内存在磁感应强度大小为B、方向垂直于纸面向里的有界匀强磁场。在紧靠P板处有一粒子源A,自t=0开始连续释放初速不计的粒子,经一段时间从Q板小孔O射入磁场,然后射出磁场,射出时所有粒子的速度方向均竖直向上。已知电场变化周期 ,粒子质量为m,电荷量为+q,不计粒子重力及相互间的作用力。求:
,粒子质量为m,电荷量为+q,不计粒子重力及相互间的作用力。求:
(1)t=0时刻释放的粒子在P、Q间运动的时间;
(2)粒子射入磁场时的最大速率和最小速率;
(3)有界磁场区域的最小面积。
如图所示,MN是匀强磁场中的一块薄金属板,带电粒子(不计重力)在匀强磁场中运动并穿过金属板(穿过金属板速度要变小),虚线表示其运动轨迹,上方和下方的磁感应强度分为B1、B2,且B1=3B2,ce=2ac。由图知:( )
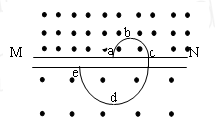
| A.粒子带负电 |
| B.粒子运动方向是abcde |
| C.粒子运动方向是edcba |
| D.粒子在上半周所用时间大于下半周所用时间 |
如图在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为B/2的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在上方运动半径为R则( )
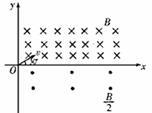
| A.粒子经偏转一定能回到原点O |
| B.粒子在x轴上方和下方两磁场中运动的半径之比为2:1 |
C.粒子完在成一次周期性运动的时间为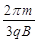 |
| D.粒子第二次射入x轴上方磁场时,沿x轴前进3R |
如图所示,左侧装置内存在着匀强磁场和方向竖直向下的匀强电场,装置上下两极板间电势差为U,间距为L,右侧为“梯形”匀强磁场区域ACDH,其中,AH//CD, 。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“梯形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“梯形”宽度
。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“梯形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“梯形”宽度 ,忽略电场、磁场的边缘效应及粒子间的相互作用。
,忽略电场、磁场的边缘效应及粒子间的相互作用。
(1)判定这束粒子所带电荷的种类,并求出粒子速度的大小;
(2)求出这束粒子可能的质量最小值和最大值;
(3)求出(2)问中偏转角度最大的粒子在“梯形”区域中运动的时间。
如图所示的平面直角坐标系 ,在第一象限内有平行于
,在第一象限内有平行于 轴的匀强电场,方向沿
轴的匀强电场,方向沿 轴负方向;在第四象限的正方形
轴负方向;在第四象限的正方形 区域内有匀强磁场,方向垂直于
区域内有匀强磁场,方向垂直于 平面向外,正方形边长为L,且
平面向外,正方形边长为L,且 边与
边与 轴平行。一质量为
轴平行。一质量为 、电荷量为
、电荷量为 的粒子,从
的粒子,从 轴上的
轴上的 点,以大小为
点,以大小为 的速度沿
的速度沿 轴正方向射入电场,通过电场后从
轴正方向射入电场,通过电场后从 轴上的
轴上的 点进入磁场,最后从
点进入磁场,最后从 点离开磁场,且速度方向与
点离开磁场,且速度方向与 边成
边成 角,不计粒子所受的重力,求:
角,不计粒子所受的重力,求:
(1)判断粒子带电的电性,并求电场强度E的大小;
(2)粒子到达 点时速度
点时速度 的大小和方向;
的大小和方向;
(3)求 区域内磁场的磁感应强度B。
区域内磁场的磁感应强度B。
如图所示,在y轴右侧有一方向垂直纸面向里的有界匀强磁场区域(图中未画出),磁感应强度大小为B。一束质量为m电量为+q的粒子流,沿x轴正向运动,其速度大小介于v0与2v0之间,从坐标原点射入磁场,经磁场偏转后,所有粒子均沿y轴正方向射出磁场区域。不计粒子重力。
求
(1)粒子在磁场中运动的最大半径和最小半径。
(2)粒子在磁场中运动的时间。
(3)满足条件的磁场区域的最小面积。
如图所示,正方形abcd区域内有垂直于纸面向里的匀强磁场,O点是cd边的中点。 一个带正电的粒子(重力忽略不计)从O点沿纸面以垂直于cd边的速度射入正方形区域内,经过时间t0刚好从c点射出磁场。现设法使该带电粒子从O点沿纸面以与Od成30°的方向(如图中虚线所示),以各种不同的速率射入正方形内,那么下列说法正确的是
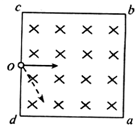
| A.该带电粒子不可能刚好从正方形的某个顶点射出磁场 |
| B.若该带电粒子从ab边射出磁场,它在磁场中经历的时间可能是t0 |
C.若该带电粒子从bc边射出磁场,它在磁场中经历的时间可能是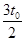 |
D.若该带电粒子从cd边射出磁场,它在磁场中经历的时间一定是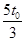 |
如图所示,S处有一电子源,可向纸面内任意方向发射电子,平板MN垂直于纸面,在纸面内的长度L=9.1cm,中点O与S间的距离d=4.55cm,MN与SO直线的夹角为θ,板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度B=2.0×10﹣4T.电子质量m=9.1×10﹣31kg,电量e=1.6×10﹣19C,不计电子重力.电子源发射速度v=1.6×106m/s的一个电子,该电子打在板上可能位置的区域的长度为l,则( )
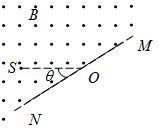
| A.θ=90°时,l=9.1cm | B.θ=60°时,l=9.1cm |
| C.θ=45°时,l=4.55cm | D.θ=30°时,l=4.55cm |
试题篮
()