高中物理质谱仪和回旋加速器的工作原理试题

一个用于加速质子的回旋加速器,其D形盒半径为R,垂直D形盒底面的匀强磁场的磁感应强度为B,接在D形盒上的高频电源频率为f.下列说法正确的是(　　)

A．质子被加速后的最大速度不可能超过2πfR

B．质子被加速后的最大速度与加速电压的大小无关

C．只要R足够大,质子的速度可以被加速到任意值

D．不需要改变任何量,这个装置也能用于加速α粒子

回旋加速器是用来加速一群带电粒子使它们获得很大动能的仪器，其核心部分是两个D形金属扁盒.两盒分别和一高频交流电源两极相连，以便在盒间的窄缝中形成匀强电场，使粒子每次穿过狭缝都得到加速.两盒放在匀强磁场中，磁场方向垂直于盒底面，粒子源置于盒的圆心附近.若粒子源射出的离子电荷量为q、质量为m，粒子最大回旋半径为R_m，其运动轨迹如图5所示,问:

图5
（1）盒内有无电场？
（2）粒子在盒内做何种运动？
（3）所加交流电频率应是多大？粒子角速度为多大？
（4）粒子离开加速器时速度为多大？最大动能为多少？
（5）设两D形盒间电场的电势差为U，盒间距离为d，其电场均匀，求加速到上述能量所需的时间.

图4是测量带电粒子质量的仪器的工作原理示意图.设法使某有机化合物的气态分子导入图中所示的容器A中，使它受到电子束轰击，失去一个电子变为正一价的分子离子.分子离子从狭缝S₁以很小的速度进入电压为U的加速电场区（初速不计），加速后，再通过狭缝S₂、S₃射入磁感应强度为B的匀强磁场，方向垂直于磁场区的界面PQ.最后，分子离子打到感光片上，形成垂直于纸面且平行于狭缝S₃的细线.若测得细线到狭缝S₃的距离为d，试导出分子离子的质量m的表达式.

图4

如图所示，回旋加速器D形盒的半径为r，匀强磁场的磁感应强度为B.一个质量为m、电荷量为q的粒子在加速器的中央从速度为零开始加速.根据回旋加速器的这些数据，估算出该粒子离开加速器时获得的动能为________________.

如图15-5-20所示，有a、b、c、d四个离子，它们带同种电荷且电荷量相等，它们的速率关系为v_a＜v_b=v_c＜v_d，质量关系为m_a=m_b＜m_c=m_d.进入速度选择器后，有两种离子从速度选择器中射出，由此可以判定(    )

图15-5-20

A．射向P1的是a粒子	B．射向P2的是b粒子
C．射向A1的是c粒子	D．射向A2的是d粒子

如图所示，一质量为m，电荷量为q的粒子从容器A下方小孔S₁飘入电势差为U的加速电场，然后让粒子垂直进入磁感应强度为B的磁场中，最后打到底片D上.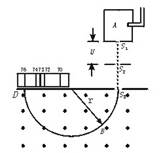

(1)粒子进入磁场时的速率。
(2)求粒子在磁场中运动的轨道半径。

如图所示是一个回旋加速器的示意图，其中两个半圆形金属盒内有方向垂直于纸面，磁感强度为B的匀强磁场，两金属盒分别接到交变电源的两极上，在两盒间的狭缝处形成交变的电场．质量为m、电量为q的带电粒子从下面盒的中心O点进入，进入时的初速可以忽略，经两盒间狭缝处的电场加速后进入上面盒内，在磁场中做圆周运动，当它回到狭缝处时，电场恰好反向，再次对粒子加速，进入下面磁场中，从c₁处再进入电场中加速，以后则重复前面的过程，并且每次电场对粒子做的功都是W．图中c₂、c₃、……是后面各次从下面磁场中射出时的位置．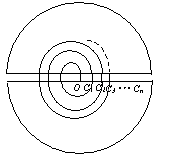

(1)求Oc₁的距离．
(2)n为多大时，c_nc_n+1小于或等于Oc₁的一半？
 

如图为质谱仪测定带电粒子质量的装置的示意图．滤速器中场强E方向向下，磁感强度的方向垂直纸面向里，分离器中磁感强度的方向垂直纸面向外．在S处有甲、乙、丙、丁四个一价正离子垂直于E和入射，若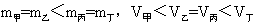，不计重力，则分别打在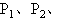四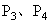点的离子分别是　[　　]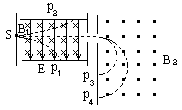

A．甲乙丙丁	B．甲丁乙丙
C．丙丁乙甲	D．甲乙丁丙

 

质谱仪是一种测定带电粒子质量和分析同位素的重要工具，它的构造原理如图所示．离子源S产生的各种不同正离子束(速度可看作为零)，经加速电场(加速电场极板间的距离为d、电势差为U)加速，然后垂直进入磁感应强度为B的有界匀强磁场中做匀速圆周运动，最后到达记录它的照相底片P上．设离子在P上的位置与入口处S₁之间的距离为x。
(1)求该离子的荷质比．
(2)若离子源产生的是带电量为q、质量为m₁和m₂的同位素离子(m₁> m₂)，它们分别到达照相底片上的P₁、P₂位置(图中末画出)，求P₁、P₂间的距离△x。
(3)若第(2)小题中两同位素离子同时进入加速电场，求它们到达照相底片上的时间差△t(磁场边界与靠近磁场边界的极板间的距离忽略不计)．

如图所示为一种质谱仪示意图，由加速电场、静电分析器和磁分析器组成。已知：静电分析器通道的半径为R，均匀辐射电场的场强为E。磁分析器中有垂直纸面向外的匀强磁场，磁感强度为B。问：（1）为了使位于A处电量为q、质量为m的离子，从静止开始经加速电场加速后沿图中圆弧虚线通过静电分析器，加速电场的电压U应为多大？（2）离子由P点进入磁分析器后，最终打在乳胶片上的Q点，该点距入射点P多远？

图甲所示为回旋加速器的原理示意图，一个扁圆柱形的金属盒子，盒子被分成两半（D形电极），分别与高压交变电源的两极相连，在裂缝处形成一个交变电场，高压交流电源的U－t图象如图乙所示，图中U（×10⁴V），t (×10^－7s)，在两D形电极裂缝的中心靠近其中一个D形盒处有一离子源Ｋ，D形电极位于匀强磁场中，磁场方向垂直于D形电极所在平面，由下向上。从离子源K发出的氘核，在电场作用下，被加速进入盒中．又由于磁场的作用，沿半圆形的轨道运动，并重新进入裂缝。这时恰好改变电场方向，氘核在电场中又一次加速，如此不断循环进行，最后在D形盒边缘被特殊装置引出。（忽略氘核在裂缝中运动的时间）

（1）写出图乙所示的高压交流电源的交流电压瞬时值的表达式；
（2）将此电压加在回旋加速器上，给氘核加速，则匀强磁场的磁感强度应为多少?
（3）若要使氘核获得5.00MeV的能量，需要多少时间?（设氘核正好在电压达到峰值时通过D形盒的狭缝）
（4）D形盒的最大半径R。

回旋加速器的D形盒半径为R＝60cm，两盒间距1cm，用它加速质子时可使每个质子获得4MeV的能量，加速电压为．求：
　　（1）该加速器中偏转磁场的磁感应强度B；
　　（2）质子在D型盒中运动的时间t；
（3）整个加速过程中，质子在电场中运动的总时间．

（1）所加交流电频率应是多大？
（2）离子离开加速器时动能多大？
（3）若两D型盒间距为d，两者间电场为匀强电场，假设粒子在电场中加速的时间不忽略，但又不影响高频电源与粒子偏转间的同步关系，求某个粒子从加速开始到从D形盒中出来，所需的总时间？

有一回旋加速器，两个D形盒的半径为R，两D形盒之间的高频电压为U，偏转磁场的磁感强度为B。如果一个α粒子和一个质子，都从加速器的中心开始被加速，试求它们从D形盒飞出时的速度之比。

回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电极相连接的两个D形金属盒，两盒间的狭缝中形成的周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，如图所示，要增大带电粒子射出时的动能，则下列说法中正确的是 （   ） 

A．增大匀强电场间的加速电压

B．增大磁场的磁感应强度

C．减小狭缝间的距离

D．增大D形金属盒的半径