高中物理全反射试题

如图甲所示是由透明材料制成的半圆柱体，一束细光束由真空沿着径向与AB成θ角射入，对射出的折射光线的强度随θ角的变化进行记录，得到的关系如图乙所示，如图丙所示是这种材料制成的器具，左侧是半径为R的半圆，右侧是长为8R，高为2R的长方体，一束单色光从左侧A′点沿半径方向与长边成37°角射入器具．已知光在真空中的传播速度为c，求：（sin37°=0.6，cos37°=0.8）

①该透明材料的折射率；
②光线至少要经过几次全反射才能穿过器具？并求出穿过器具所用的时间？（必须有必要的计算说明）

如图所示，ABCD是一直角梯形棱镜的横截面，位于截面所在平面内的一束光线由O点垂直AD边射入。已知棱镜的折射率，AB=BC=8cm，OA=2cm，∠OAB=60⁰

(i)求光线第一次射出棱镜时，出射光线的方向;
(ii)第一次的出射点距C点的距离.

如图所示，一个折射率为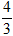的三棱镜的截面为等腰直角△ABC，∠A为直角。此截面所在平面内的一束光线沿与AB边成θ角（θ＜90°）的方向入射到AB边的中点P处，若要光线进入三棱镜后能射到AC边上且能在AC面上发生全反射，则cosθ应满足什么条件？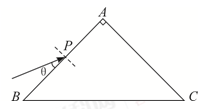

一赛艇停在平静的水面上，赛艇前端有一标记P离水面的高度为h₁=0.6m，尾部下端Q略高于水面，赛艇正前方离赛艇前端s₁=0.8m处有一浮标，示意如图．一潜水员在浮标前方s₂=3.0m处下潜到深度为h₂=4.0m时，看到标记刚好被浮标挡住，此处看不到船尾端Q，继续下潜△h=4.0m，恰好能看见Q．求：

（1）水的折射率n；
（2）赛艇的长度1．（可用根式表示）

两束平行的光斜射到平行玻璃砖，经玻璃砖折射后如图所示，则关于这两束光的说法中正确的是

A．A光的折射率比B光的折射率小

B．从玻璃砖下表面射出的两束光可能不平行

C．A光在水中的传播速度比B光在水中的传播速度小

D．增大A光在上界面的入射角，则进入玻璃砖的光线在下界面不可能发生全反射

如图所示，横截面为直角三角形的玻璃砖ABC，AC边长为L，，光线P、Q同时由AC中点射入玻璃砖，其中光线P方向垂直AC边，光线Q方向与AC边夹角为，发现光线Q第一次到达BC边后垂直BC边射出，光速为c，求：

①玻璃砖的折射率；
②光线P由进入玻璃砖到第一次由BC边出射经历的时间

如图甲所示的由透明材料制成的半圆柱体，一束细光束由真空沿着径向与AB成角射入，对射出的折射光线的强度随角的变化进行记录，得到的关系如图乙所示，如图丙所示是这种材料制成的器具，左侧是半径为R的半圆，右侧是长为8R，高为2R的长方体，一束单色光从左侧点沿半径方向与长边成37°角射入器具，已知光在真空中的传播速度为c，求：（sin37°=0.6，cos37°=0.8）

①该透明材料的折射率
②光线至少要经过几次全反射才能穿过器具？并求出器具所用的时间？（必须有必要的计算说明）

截面为等腰直角三角形的三棱镜如图甲所示。 $\mathit{DE}$ 为嵌在三棱镜内部紧贴 $\mathit{BB}\text{'}C\text{'}C$ 面的线状单色可见光光源， $\mathit{DE}$ 与三棱镜的 $\mathit{ABC}$ 面垂直， $D$ 位于线段 $\mathit{BC}$ 的中点。图乙为图甲中 $\mathit{ABC}$ 面的正视图。三棱镜对该单色光的折射率为 $\sqrt{2}$ ，只考虑由 $\mathit{DE}$ 直接射向侧面 $A{A}^{\text{'}}{C}^{\text{'}}C$ 的光线。下列说法正确的是 $($ 　　 $)$

A．	光从 $\mathit{AA}\text{'}C\text{'}C$ 面出射的区域占该侧面总面积的 $\frac{1}{2}$
B．	光从 $\mathit{AA}\text{'}C\text{'}C$ 面出射的区域占该侧面总面积的 $\frac{1}{3}$
C．	若 $\mathit{DE}$ 发出的单色光频率变小， $\mathit{AA}\text{'}C\text{'}C$ 面有光出射的区域面积将增大
D．	若 $\mathit{DE}$ 发出的单色光频率变小， $\mathit{AA}\text{'}C\text{'}C$ 面有光出射的区域面积将减小

与通常观察到的月全食不同,小虎同学在2012年12月10日晚观看月全食时,看到整个月亮是暗红的。小虎画了月全食的示意图,并提出了如下猜想,其中最为合理的是

A．地球上有人用红色激光照射月球

B．太阳照射到地球的红光反射到月球

C．太阳光中的红光经地球大气层折射到月球

D．太阳光中的红光在月球表面形成干涉条纹

如图所示，将一等腰直角棱镜ABC截去棱角ADE，使其截面DE平行于底面BC，可制成“道威棱镜”，这样就减小了棱镜的重量和杂散的内部反射。已知棱镜玻璃的折射率n＝，棱边长cm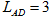，cm，一束平行于底边BC的单色光从DE边上的M点射入棱镜，求：

（i）光线进入“道威棱镜”时的折射角；
（ii）通过计算判断光线能否从BC边射出；
（ⅲ）光线在棱镜中传播所用的时间。

（1）由波源S形成的简谐横波在均匀介质中向左、右传播。波源振动的频率为20 Hz，波速为16 m/s。已知介质中P、Q两质点位于波源S的两侧，且P、Q和S的平衡位置在一条直线上，P、Q的平衡位置到S的平衡位置之间的距离分别为15．8 m、14．6 m，P、Q开始震动后，下列判断正确的是_____。

A．	P、Q两质点运动的方向始终相同
B．	P、Q两质点运动的方向始终相反
C．	当S恰好通过平衡位置时，P、Q两点也正好通过平衡位置
D．	当S恰好通过平衡位置向上运动时，P在波峰
E．	当S恰好通过平衡位置向下运动时，Q在波峰

（2）如图，玻璃球冠的折射率为 $\sqrt{3}$ ，其底面镀银，底面的半径是球半径的 $\frac{\sqrt{3}}{2}$ 倍；在过球心O且垂直于底面的平面（纸面）内，有一与底面垂直的光线射到玻璃球冠上的M点，该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。

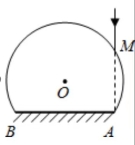
如图所示，一束截面为圆形（半径R）的平行白光垂直射向一玻璃半球的平面，经折射后在屏幕S上形成一个圆形彩色亮区。已知玻璃半球的半径为R，屏幕S至球心的距离为d（d>3R），不考虑光的干涉和衍射，试问：

①在屏幕S上形成的圆形亮区的最外侧是什么颜色?
②若玻璃半球对最外侧色光的折射率为，求出圆形亮区的最大半径。

半径为R的固定半圆形玻璃砖的横截面如图所示，O点为圆心，OO′为直径MN的垂线．足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直．一束复色光沿半径方向与OO′成θ＝30°角射向O点，已知复色光包含有折射率从n₁＝到n₂＝的光束，因而光屏上出现了彩色光带．

（1）求彩色光带的宽度；
（2）当复色光入射角逐渐增大时，光屏上的彩色光带将变成一个光点，求θ角至少为多少？

如图所示为某种透明介质的截面图，ACB为半径R=10cm的二分之一圆弧，AB与水平面屏幕MN垂直并接触于A点。由红光和紫光两种单色光组成的复色光射向圆心O，在AB分界面上的入射角i=45°，结果在水平屏幕MN上出现两个亮斑。已知该介质对红光和紫光的这首率分别为，。

i. 判断在AM和AN两处产生亮斑的颜色；
ii. 求两个亮斑间的距离。

如图所示为一透明玻璃半球，在其下面有一平行半球上表面水平放置的光屏。两束关于中心轴OO＇对称的激光束从半球上表面垂直射入玻璃半球，恰能从球面射出。当光屏距半球上表面h₁=40cm时，球面折射出的两束光线汇聚于光屏与OO＇轴的交点，当光屏距上表面h₂=70cm时，在光屏上形成半径r=40cm的圆形光斑。求该半球形玻璃的折射率。