图中方框区域内有一个位置可任意摆放的全反射棱镜,其横截面是等腰直角三角形.光线1、2、3、4所表示的入射光束经此棱镜后,相应的出射光线是1'、2'、3'、4'.图示的4种情形中,哪些是可能实现的?
(4分)利用光的现象或原理填空
| A.照相机镜头镀的一层膜是利用了光的________原理 |
| B.海市蜃楼是光的________现象 |
| C.光纤通信是利用了光的________原理 |
| D.人们眯起眼看灯丝时会看到彩色条纹,这是光的________现象 |
1966年华裔科学家高锟博士提出一个理论:直径仅几微米的玻璃纤维就可以用来做为光的波导来传输大量信息,43年后高锟因此获得2009年诺贝尔物理学奖,他被誉为“光纤通讯之父”。光导纤维的结构如图所示,其内芯和外套材料不同,光在内芯中传播。内芯的折射率 外套的折射率(填“大于”、“等于”或“小于”),光在光导纤维中传输的原理是利用了光的 现象。
某介质对红光的折射率为n1,红光在该介质中的速度为v1,波长为λ1,发生全反射的临界角为C1,该介质对紫光的折射率为n2,,紫光在该介质中的速度为v2, 波长为λ2发生全反射的临界角为C2,则n1 n2;λ1 λ2;v1 v2;C1 C2。(填<,>或=)
黄、红、绿三种单色光以相同的入射角到达介质和空气的界面.若黄光恰好发生全反射,则下列说法正确的是( )
| A.绿光一定能发生全反射 |
| B.红光一定能发生全反射 |
| C.绿光在该介质中波长最短 |
| D.只有红光从介质进入空气 |
如图所示,光线由空气射入玻璃砖,玻璃砖的AC.BD两个端面与AB.CD面垂直,入射点O的位置不变,入射光线的方向可以任意变化.下列说法正确的是
A.光线在AB界面上不可能出现全反射
B.光线在CD界面上不可能出现全反射
C.光线在BD界面上可能出现全反射
D.光线在BD界面上不可能出现全反射
一个半径为 的薄软木圆片,在它的圆心处插入一枚大头针。让它们浮在水面上,如图所示。调整大头针露出的长度,直至从水面上方的各个方向向水中看,都恰好看不到大头针,这是因为发生了__________现象。若此时木片下方大头针的长度为h,则水的折射率为__________。
的薄软木圆片,在它的圆心处插入一枚大头针。让它们浮在水面上,如图所示。调整大头针露出的长度,直至从水面上方的各个方向向水中看,都恰好看不到大头针,这是因为发生了__________现象。若此时木片下方大头针的长度为h,则水的折射率为__________。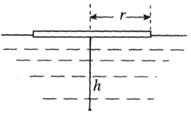
a、b两种单色光组成的光束从介质进入空气时,其折射光束如图所示。若用a、b两束光先后照射某金属,b光照射时恰能逸出光电子;那么a光照射时金属板 (填“能”或“不能”)逸出光电子;现将a、b两束光先后从同一介质以相同方向射向空气,其界面为平面,若b光不能进入空气,则a光 (填“能”或“不能”)进入空气。
一个横截面为矩形、粗细均匀的折射率为n的玻璃棒,被弯成如图所示的半圆形状,其内半径为 ,玻璃棒横截面宽为
,玻璃棒横截面宽为 。如果一束平行光垂直于玻璃棒水平端面
。如果一束平行光垂直于玻璃棒水平端面 射入,并使之全部从水平端面
射入,并使之全部从水平端面 射出,则
射出,则 与
与 的最小比值为________________。
的最小比值为________________。 
如图13-7-9所示,一束平行光从真空射向一块半圆形的玻璃砖,下列说法正确的是( )
图13-7-9
| A.只有圆心两侧一定范围内的光线不能通过玻璃砖 |
| B.只有圆心两侧一定范围内的光线能通过玻璃砖 |
| C.通过圆心的光线将沿直线穿过玻璃砖不发生偏折 |
| D.圆心两侧一定范围外的光线将在曲面产生全反射 |
已知介质对某单色光的临界角为C,则( )
A.该介质对单色光的折射率等于 |
| B.此单色光在该介质中的传播速度等于c·sinC(c是光在真空中的传播速度) |
| C.此单色光在该介质中的波长是在真空中波长的sinC倍 |
D.此单色光在该介质中的频率是在真空中的 倍 倍 |
如图14-1-18所示,一束光从空气射向折射率n=2的玻璃表面.若以i表示入射角,则( )
图14-1-18
| A.当i>45°时会发生全反射现象 |
| B.无论i多大,折射角r都不会超过45° |
| C.为了使折射角r=30°,应以i=45°的角度入射 |
| D.当入射角i=arctan2时,反射光线与折射光线垂直 |
某种单色光在一种透明介质中传播速度是1.5×108m/s,在这种介质中的波长是3×10-7m,此介质对该单色光的折射率为_____,该单色光的频率是____ Hz ,这种单色光从此介质中射入真空发生全反射的临界角是______。
试题篮
()