高中物理电火花计时器、电磁打点计时器计算题

如图所示，通电导体棒AC静止于水平导轨上，棒的质量为m长为L，通过的电流强度为I，匀强磁场的磁感强度B的方向与导轨平面成θ角，求导轨受到AC棒的压力和摩擦力各为多大？

电荷量为q=1×10^－4C的带正电小物块置于粗糙的绝缘水平面上，所在空间存在沿水平方向的匀强电场，场强E与时间t的关系及物块速度v与时间t的关系如图所示。若重力加速度g取10 m/s²，求：（1）物块的质量m以及物块与水平面之间的动摩擦因数；（2）物块运动2s过程中，其电势能的改变量。

如图所示，A、B是竖直放置的中心带有小孔的平行金属板，两板间的电压为U₁=100V，C、D是水平放置的平行金属板，板间距离为d=0.2m，板的长度为L=1m，P是C板的中点，A、B两板小孔连线的延长线与C、D两板的距离相等，将一个负离子从板的小孔处由静止释放，求：

（1）为了使负离子能打在P点，C、D两板间的电压应为多少？哪板电势高？
（2）如果C、D两板间所加的电压为2V，则负离子能打在板上吗？若不能打在板上，它离开电场时发生的侧位移多少？

如图所示,半径为R的光滑绝缘环，竖直放置于电场强度为E的水平匀强电场中，质量为m，带电量为+q的空心小球穿在环上。当小球由静止开始从环的顶点A下滑到与圆心等高的水平位置B时，求：

(1)小球的电势能变化多大？
(2)小球的速度是多大？
(3)小球对环的压力多大？

一束电子流在经U＝5000 V的加速电压加速后，在距两极板等距处以速度v₀垂直进入平行板间的匀强电场，如图所示，若两板间距d="1.0" cm，板长l="5.0" cm，

（1）当两极板所加电压一定时，电子能从平行板间飞出试证明电子的侧移量y与电子的电量m, 质量 q无关。
（2）要使电子能从平行板间飞出，两个极板上最多能加多大电压?
（3）要使电子能打在下板的中点A处，两个极板所加的电压?

在长为2L的绝缘轻质细杆的两端各连接一个质量均为m的带电小球A和B（可视为质点，也不考虑二者间的相互作用力），A球带正电、电荷量为+2q，B球带负电。电荷量为－3q。现把A和B组成的带电系统锁定在光滑绝缘的水平面上，并让A处于如图所示的有界匀强电场区域MPQN内。已知虚线MP是细杆的中垂线，MP和NQ的距离为4L，匀强电场的场强大小为E，方向水平向右。现取消对A、B的锁定，让它们从静止开始运动。（忽略小球运动中所产生的磁场造成的影响）

（1）求小球A、B运动过程中的最大速度；
（2）小球A、B能否回到原出发点？若不能，请说明理由；若能，请求出经过多长时间带电系统又回到原地发点。
（3）求运动过程中带电小球B电势能增加的最大值。

如图所示，绝缘的水平桌面上方有一竖直方向的矩形区域，该区域是由三个边长均为L的正方形区域ABFE、BCGF和CDHG首尾相接组成的，且矩形的下边EH与桌面相接．三个正方形区域中分别存在方向为竖直向下、竖直向上、竖直向上的匀强电场，其场强大小比例为1:1:2．现有一带正电的滑块以某一初速度从E点射入场区，初速度方向水平向右，滑块最终恰从D点射出场区．已知滑块在ABFE区域所受静电力和所受重力大小相等，桌面与滑块之间的滑动摩擦因素为0.125，重力加速度为g，滑块可以视作质点．求：

（1）滑块进入CDHG区域时的速度大小．
（2）滑块在ADHE区域运动的总时间．

如图甲所示，边长为L的正方形区域A BCD内有竖直向下的匀强电场，电场强度为E，与区域边界BC相距L处竖直放置足够大的荧光屏，荧光屏与AB延长线交于O点.现有一质量为m，电荷量为+q的粒子从A点沿AB方向以一定的初速度进入电场，恰好从BC边的中点P飞出，不计粒子重力.

(1)求粒子进入电场前的初速度的大小.
(2)其他条件不变，增大电场强度使粒子恰好能从CD边的中点Q飞出，求粒子从Q点飞出时的动能.
(3)现将原来电场分成AEFD和EBCF相同的两部分，并将EBCF向右平移一段距离x(x≤L)，如图乙所示.设粒子打在荧光屏上位置与O点相距y，请求出y与x的关系.

如图所示，间距l＝0.3 m的平行金属导轨a₁b₁c₁和a₂b₂c₂分别固定在两个竖直面内．在水平面a₁b₁b₂a₂区域内和倾角θ＝37°的斜面c₁b₁b₂c₂区域内分别有磁感应强度B₁＝0.4 T，方向竖直向上和B₂＝1 T、方向垂直于斜面向上的匀强磁场．电阻R＝0.3 Ω、质量m₁＝0.1 kg、长为l的相同导体杆K、S、Q分别放置在导轨上，S杆的两端固定在b₁、b₂点，K、Q杆可沿导轨无摩擦滑动且始终接触良好．一端系于K杆中点的轻绳平行于导轨绕过轻质定滑轮自然下垂，绳上穿有质量m₂＝0.05 kg的小环．已知小环以a＝6 m/s²的加速度沿绳下滑，K杆保持静止，Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动．不计导轨电阻和滑轮摩擦，绳不可伸长．取g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8.

求(1)小环所受摩擦力的大小；
(2)Q杆所受拉力的瞬时功率．

如图所示，水平绝缘光滑轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接，圆弧的半径R=0.40m。在轨道所在空间存在水平向右的匀强电场，电场强度E =1.0×10⁴ N/C。现有一质量m=0.10kg的带电体（可视为质点）放在水平轨道上与B端距离s=1.0m的位置，由于受到电场力的作用带电体由静止开始运动，当运动到圆弧形轨道的C端时，速度恰好为零。已知带电体所带电荷q=8.0×10^-5C，取g=10m/s²，求：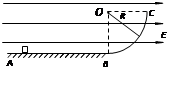

（1）带电体在水平轨道上运动的加速度大小及运动到B端时的速度大小；
（2）带电体运动到圆弧形轨道的B端时对圆弧轨道的压力大小；
（3）带电体沿圆弧形轨道运动过程中，电场力和摩擦力对带电体所做的功各是多少。

如图所示，在场强E=1×10⁴N/C的水平匀强电场中，有一根长为L=15cm的细线，一端固定在O点，另一端系一个质量m=3g、带电量q=+2×10^－6C的小球，当细线处于水平位置，小球在A点从静止开始释放，求：小球到达最低点B时对细线的拉力大小。

质谱仪是一种测定带电粒子质量和分析同位素的重要工具.它的构造原理如图所示，离子源S产生电荷量为q的某种正离子，离子产生时的速度很小，可以看作是静止的，离子经过电压U加速后形成离子流，然后垂直于磁场方向进入磁感应强度为B的匀强磁场，沿着半圆周运动而到达记录它的照相底片P上.实验测得，它在P上的位置到入口处S₁的距离为a，离子流的电流为I.请回答下列问题:

(1)在时间t内到达照相底片P上的离子的数目为多少？
(2)单位时间内穿过入口S₁处离子流的能量为多大？
(3)试求这种离子的质量m？.

竖直放置的半圆形光滑绝缘管道处在如图所示的匀强磁场中，B=1.1T，管道半径R=0.8m，其直径POQ在竖直线上，在管口P处以2m／s的速度水平射入一个带电小球，可把它视为质点，其电荷量为lO^-4C(g=lOm／s²)，试求：

(1)小球滑到Q处的速度为多大?
(2)若小球从Q处滑出瞬间，管道对它的弹力正好为零，小球的质量为多少?

质量m=2．0×10^-4kg、电荷量q=1．0×10^-6C的带正电微粒悬停在空间范围足够大的匀强电场中，电场强度大小为E₁．在t=0时刻，电场强度突然增加到E₂=4．0×10³N/C，场强方向保持不变．到t=0．20s时刻再把电场方向改为水平向右，场强大小保持不变．取g=10m/s²．求：
（1）原来电场强度E₁的大小？
（2）t=0．20s时刻带电微粒的速度大小？
（3）带电微粒运动速度水平向右时刻的动能？

如图所示，水平固定放置的两根平行光滑导轨MN、PQ，两导轨间距L＝0.50 m，导轨间接有电阻R＝0.50Ω．一导体棒ab垂直跨放在导轨上，现在力F的作用下在导轨上匀速滑动。已知除电阻R外，导体棒ab和导轨的电阻都可忽略不计，匀强磁场垂直框架平面向里，磁感应强度，B＝0.40 T．导轨足够长．当ab以v＝4.0 m/s的速度向右匀速滑动时，（g=10m/s²）

求：(1)ab棒中产生的感应电动势大小；
(2)维持导体棒ab做匀速运动的外力F的大小．