放置在同一竖直面内的两光滑同心圆环a、b通过过其圆心的竖直轴O1O2连接，其半径Rb=
Ra，环上各有一个穿孔小球A、B(图中B球未画出)，均能沿环无摩擦滑动。如果同心圆环绕竖直轴O1O2以角速度ω匀速旋转，两球相对于铁环静止时，球A所在半径OA与O1O2成θ=300角。则( )
A.球B所在半径OB与O1O2成45°角
B.球B所在半径OB与O1O2成30°角
C.球B和球A在同一水平线上
D.由于球A和球B的质量未知，不能确定球B的位置
“超级地球”是指围绕恒星公转的类地行星 科学家们发现有两颗未知质量的不同“超级地球”环绕同一颗恒星公转，周期分别为10天和20天 根据上述信息可以计算两颗“超级地球”（ ）
A 质量之比
B 所受的引力之比
C 角速度之比
D 向心加速度之比
如图所示，一可视为光滑的玻璃小球，设其可在碗内不同的水平面上做匀速圆周运动，下列说法正确的是 
| A．玻璃球越靠近碗口其对碗的压力越大 |
| B．玻璃球越靠近碗口其向心加速度越小 |
| C．玻璃球越靠近碗口其线速度一定越大 |
| D．玻璃球的重力与碗内壁对它的弹力的合力提供球做圆周运动所需的向心力 |
“嫦娥三号”探测器环绕月球运行的轨道半径为r，如果轨道半径r变大，下列说法中正确的是（ ）
| A．线速度变小 | B．角速度变大 |
| C．向心加速度变大 | D．周期变小 |
如图所示,两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中,轨道两端在同一高度上,轨道是光滑的而且绝缘,两个相同的带正电小球同时从两轨道左端最高点由静止释放,a 、b为轨道的最低点,则不正确的是
| A．两小球到达轨道最低点的速度va＞vb |
| B．两小球到达轨道最低点时对轨道的压力Fa＞Fb |
| C．小球第一次到达a点的时间大于小球第一次到达b点的时间 |
| D．在磁场中小球能到达轨道的另一端,在电场中小球不能到达轨道的另一端 |
如图所示，一半径为，粗糙程度处处相同的半圆形轨道竖直固定放置,直径
水平。一质量为
的质点自
点上方高度
处由静止开始下落，恰好从
点进入轨道。质点滑到轨道最低点
时，对轨道的压力为
，
为重力加速度的大小。用
表示质点从
点运动到
点的过程中客服摩擦力所做的功。则（）
| A． |
 ，质点恰好可以到达
|
| B． |
 ，质点不能到达
|
| C． |
，质点到达
|
| D． |
 ，质点到达
|
如图所示，足够大的光滑绝缘水平面上有三个带电质点M、O、N，质点O恰能保持静止，质点M、N均围绕质点O做匀速圆周运动。已知质点M、N与质点O的距离分别为L1、L2。不计质点间的万有引力作用。下列说法中正确的是（ ）
| A．质点M与质点N带有异种电荷 |
| B．质点M与质点N的线速度相同 |
C．质点M与质点N的质量之比为 |
| D．质点M与质点N所带电荷量之比为 |
半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球，现给小球一个冲击使其在瞬间得到一个水平初速度v0，若v0大小不同，则小球能够上升到的最大高度(距离底部)也不同．下列说法中正确的是（ ）
A．如果v0＝ ，则小球能够上升的最大高度等于R/2 |
B．如果v0＝ ，则小球能够上升的最大高度小于3R/2 |
C．如果v0＝ ，则小球能够上升的最大高度等于2R |
D．如果v0＝ ，则小球能够上升的最大高度等于2R |
如图所示，甲、乙两水平圆盘紧靠在一块，甲圆盘为主动轮，乙靠摩擦随甲无打滑转动．甲圆盘与乙圆盘的半径之比为r甲∶r乙＝2∶1，两圆盘和小物体m1、m2之间的动摩擦因数相同，m1距O点为2r，m2距O′点为r，当甲缓慢转动起来且转速慢慢增加时（ ）．
| A．与圆盘相对滑动前m1与m2的角速度之比ω1∶ω2＝2∶1 |
| B．与圆盘相对滑动前m1与m2的向心加速度之比a1∶a2＝1∶2 |
| C．随转速慢慢增加，m1先开始滑动 |
| D．随转速慢慢增加，m2先开始滑动 |
一杂技演员骑摩托车沿一竖直圆形轨道做特技表演，如图所示．A、C两点分别是轨道的最低点和最高点，B、D分别为两侧的端点， 若运动中速率保持不变，人与车的总质量为m，设演员在轨道内逆时针运动．下列说法正确的是（ ）
A．人和车的向心加速度大小不变
B．摩托车通过最低点A时，轨道受到的压力可能等于mg
C．由D点到A点的过程中，人始终处于超重状态
D．摩托车通过A、C两点时，轨道受到的压力完全相同
如图所示，一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定，有质量相等的小球A和B沿着筒的内壁在水平面内作匀速圆周运动，A的运动半径较大，则下列说法正确的是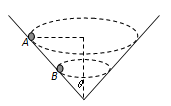
| A．球A的线速度小于球B的线速度 |
| B．球A的角速度大于球B的角速度 |
| C．球A的加速度等于球B的加速度 |
| D．球A对筒壁的压力大小大于球B对筒壁的压力大小 |
如图所示，细绳的一端固定在O点，另一端系一质量为m的小球(可视为质点)，当小球在竖直平面内沿逆时针方向做圆周运动时，通过传感器测得轻绳拉力FT与轻绳与竖直方向OP的夹角θ满足关系式FT＝a＋bcos θ，式中a、b为常数。若不计空气阻力，则当地的重力加速度为( )
A． |
B． |
C． |
D． |
赤道上随地球自转的物体A，赤道上空的近地卫星B，地球的同步卫星C，它们的运动都可以视为匀速圆周运动．分别用a、v、T、ω表示物体的向心加速度、速度、周期和角速度，下列判断正确的是（ ）
| A．aA＞aB＞aC | B．vB＞vC＞vA | C．TA＞TB＞TC | D．ωA＞ωC＞ωB |
人类向宇宙空间发展最具可能的是在太阳系内地球附近建立“太空城”。设想中的一个圆柱形太空城，其外壳为金属材料，长
，直径
，内壁沿纵向分隔成6个部分，窗口和人造陆地交错分布，陆地上覆盖
厚的土壤，窗口外有巨大的铝制反射镜，可调节阳光的射入，城内部充满空气、太空城内的空气、水和土壤最初可从地球和月球运送，以后则在太空城内形成与地球相同的生态环境。为了使太空城内的居民能如地球上一样具有“重力”，以适应人类在地球上的行为习惯，太空城将在电力的驱动下，绕自己的中心轴以一定的角速度转动。如图为太空城垂直中心轴的截面，以下说法正确的有
| A．太空城内物体所受的“重力”一定通过垂直中心轴截面的圆心 |
| B．人随太空城自转所需的向心力由人造陆地对人的支持力提供 |
| C．太空城内的居民不能运用天平准确测出质量 |
| D．太空城绕自己的中心轴转动的角速度越大，太空城的居民受到的“重力”越大 |
在一次探究活动中，某同学设计了如图所示的实验装置，将半径R="1" m的光滑半圆弧轨道固定在质量M="0.5" kg、长L="4" m的小车的上表面中点位置，半圆弧轨道下端与小车的上表面水平相切，现让位于轨道最低点的质量m="0.1" kg的光滑小球随同小车一起沿光滑水平面向右做匀速直线运动，某时刻小车碰到障碍物而瞬时处于静止状态（小车不反弹），之后小球离开圆弧轨道最高点并恰好落在小车的左端边沿处，该同学通过这次实验得到了如下结论，其中正确的是（g取10 m/s2） ( )
A．小球到达最高点的速度为 m/s |
| B．小车与障碍物碰撞时损失的机械能为12.5 J |
| C．小车瞬时静止前、后，小球在轨道最低点对轨道的压力由1 N瞬时变为6.5 N |
| D．小车向右做匀速直线运动的速度约为6.5 m/s |
试题篮
()
粤公网安备 44130202000953号
