如图所示,M、N为两平行金属板相距d="0.4" m,板间有垂直纸面的匀强磁场B="0.25" T。图中I和Ⅱ是两根与M、N平行的金属导轨,I与M相距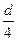 、Ⅱ与N相距
、Ⅱ与N相距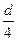 ,I与Ⅱ之间接一电阻R="0." 3Ω。现有一金属杆在上述装置上(接触良好)向右水平运动,已知金属杆ab间电阻
,I与Ⅱ之间接一电阻R="0." 3Ω。现有一金属杆在上述装置上(接触良好)向右水平运动,已知金属杆ab间电阻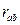 ="0." 2Ω,若有一个带电量
="0." 2Ω,若有一个带电量 C的粒子以
C的粒子以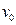 ="7" m/s沿水平向右射入MN间,恰好能匀速运动。求:
="7" m/s沿水平向右射入MN间,恰好能匀速运动。求: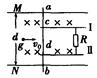
(1)两极间电势差 。
。
(2)ab杆运动速度。
(3)为保持ab杆匀速运动,所需外力F。
如图所示,两互相平行的水平金属导轨MN、PQ放在竖直平面内,相距为L="0." 4 m,左端接平行板电容器,板间距离为d="0." 2 m,右端接滑动变阻器R(R的最大阻值为2Ω,整个空间有水平匀强磁场,磁感应强度为B="10" T,方向垂直于导轨所在平面。导体棒CD与导轨接触良好,棒的电阻为r=1Ω,其他电阻及摩擦均不计,现对导体棒施加与导轨平行的大小为F="2" N的恒力作用,使棒从静止开始运动,取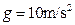 。求:
。求:
(1)当滑动变阻器R接入电路的阻值最大时,拉力的最大功率是多大?
(2)当滑动触头在滑动变阻器中点且导体棒处于稳定状态时,一带电小球从平行板电容器左侧沿两极板的正中间入射,在两极板间恰好做匀速直线运动;当滑动触头在滑动变阻器最下端且导体棒处于稳定状态时,该带电小球以同样的方式和速度入射,在两极板间恰好能做匀速圆周运动,求圆周的半径是多大?
如图所示,光滑平行金属导轨固定在绝缘水平面上,轨道间距为0. 2 m,金属杆ab的质量为0. 1 kg,电容器电容为0.5 F,耐压足够大,因为理想电流表,导轨与杆接触良好,各自的电阻忽略不计。整个装置处于磁感应强度大小为0.5 T,方向垂直导轨平面向下的匀强磁场中。现用水平外力F拉ab向右运动,使电流表示数恒为0. 5 A。
(1)求t=2s时电容器的带电量。
(2)说明金属杆做什么运动。
(3)求t=2s时外力做功的功率。
如图所示,两根足够长固定平行金属导轨位于倾角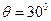 的斜面上,导轨上、下端各接有阻值R = 20Ω的电阻,导轨电阻忽略不计,导轨宽度L =2m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=1T。质量m="0." l kg、连入电路的电阻r=10Ω的金属棒ab在较高处由静止释放,当金属棒ab下滑高度h=3m时,速度恰好达到最大值v=2m/s,金属棒ab在下滑过程中始终与导轨垂直且与导轨良好接触。g取10
的斜面上,导轨上、下端各接有阻值R = 20Ω的电阻,导轨电阻忽略不计,导轨宽度L =2m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=1T。质量m="0." l kg、连入电路的电阻r=10Ω的金属棒ab在较高处由静止释放,当金属棒ab下滑高度h=3m时,速度恰好达到最大值v=2m/s,金属棒ab在下滑过程中始终与导轨垂直且与导轨良好接触。g取10 .求:
.求:
(1)金属棒ab由静止至下滑高度为3m的运动过程中机械能的减少量。
(2)金属棒ab由静止至下滑高度为3m的运动过程中导轨上端电阻R中产生的热量。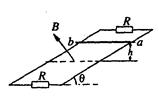
(06江苏物理卷)如图所示,顶角θ=45°,的金属导轨MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求:
(1)t时刻流过导体棒的电流强度I和电流方向。
(2)导体棒作匀速直线运动时水平外力F的表达式。
(3)导体棒在0~t时间内产生的焦耳热Q。
(4)若在t0时刻将外力F撤去,导体棒最终在导轨上静止时的坐标x。
如图所示,水平光滑平行导轨间距L=lm,左端接有阻值R=1.5 的定值电阻,在距左端
的定值电阻,在距左端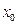 =2m处垂直导轨放置一根质量m=1kg、电阻r=0.5
=2m处垂直导轨放置一根质量m=1kg、电阻r=0.5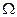 的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中。
的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中。
(1)若磁场的磁感应强度B随时间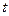 变化的关系为
变化的关系为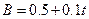 (式中B的单位为T,
(式中B的单位为T,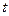 的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间
的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间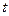 变化的规律;
变化的规律;
(2)若磁场的磁感应强度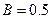 T恒定,
T恒定,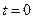 时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知
时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知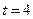 s时F=3N,求此时导体棒两端的电势差。
s时F=3N,求此时导体棒两端的电势差。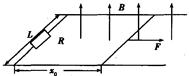
2006年7月1日,世界上海拔最高、线路最长的青藏铁路全线通车,青藏铁路安装的一种电磁装置可以向控制中心传输信号,以确定火车的位置和运动状态,其原理是将能产生匀强磁场的磁铁安装在火车首节车厢下面,如图甲所示(俯视图),当它经过安放在两铁轨间的线圈时,线圈便产生一个电信号传输给控制中心。线圈边长分别为 和
和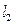 ,匝数为n,线圈和传输线的电阻忽略不计。若火车通过线圈时,控制中心接收到线圈两端的电压信号u与时间t的关系如图乙所示(ab、cd均为直线),
,匝数为n,线圈和传输线的电阻忽略不计。若火车通过线圈时,控制中心接收到线圈两端的电压信号u与时间t的关系如图乙所示(ab、cd均为直线),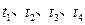 是运动过程的四个时刻,则火车( )
是运动过程的四个时刻,则火车( )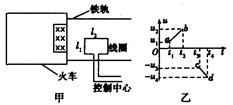
A.在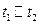 时间内做加速直线运动 时间内做加速直线运动 |
B.在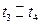 时间内做匀减速直线运动 时间内做匀减速直线运动 |
C.在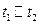 时间内加速度大小为 时间内加速度大小为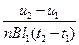 |
D.在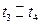 时间内平均速度的大小为 时间内平均速度的大小为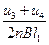 |
如图所示,两根完全相同的“V”字形导轨OPQ与KMN倒放在绝缘水平面上,两导轨都在竖直平面内且正对平行放置,其间距为L,电阻不计。两条导轨足够长,所形成的两个斜面与水平面的夹角都是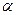 。两个金属棒ab和
。两个金属棒ab和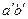 的质量都是m,电阻都是R,与
的质量都是m,电阻都是R,与 导轨垂直放置且接触良好。空间有分别垂直两斜面的匀强磁场,磁感应强度均为B。
导轨垂直放置且接触良好。空间有分别垂直两斜面的匀强磁场,磁感应强度均为B。
(1)如果两条导轨皆光滑,让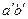 固定不动,将ab释放,则ab达到的最大速度是多少?
固定不动,将ab释放,则ab达到的最大速度是多少?
(2)如果将ab与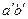 同时释放,它们所能达到的最大速度分别是多少?
同时释放,它们所能达到的最大速度分别是多少?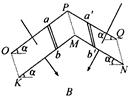
(05天津理综卷)图中MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计。导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直。质量m为6.0×10-3kg、电阻为1.0Ω的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R1。当杆ab达到稳定状态时以速率v匀速下滑,整个电路消耗的电功率P为0.27W,重力加速度取10m/s2,试求速率v和滑动变阻器接入电路部分的阻值R2。
如图()所示,光滑的平行长直金属导轨置于水平面内,间距为
、导轨左端接有阻值为
的电阻,质量为
的导体棒垂直跨接在导轨上。导轨和导体棒的电阻均不计,且接触良好。在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为
。开始时,导体棒静止于磁场区域的右端,当磁场以速度
匀速向右移动时,导体棒随之开始运动,同时受到水平向左、大小为
的恒定阻力,并很快达到恒定速度,此时导体棒仍处于磁场区域内。


(1)求导体棒所达到的恒定速度;
(2)为使导体棒能随磁场运动,阻力最大不能超过多少?
(3)导体棒以恒定速度运动时,单位时间内克服阻力所做的功和电路中消耗的电功率各为多大?
(4)若时磁场由静止开始水平向右做匀加速直线运动,经过较短时间后,导体棒也做匀加速直线运动,其
关系如图(
)所示,已知在时刻
导体棒瞬时速度大小为
,求导体棒做匀加速直线运动时的加速度大小。
磁悬浮列车的运动原理如图所示,在水平面上有两根很长的平行直导轨,导轨间有与导轨垂直且方向相反的匀强磁场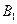 和
和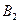 ,
,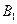 和
和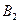 相互间隔,导轨上有金属框abcd。当磁场
相互间隔,导轨上有金属框abcd。当磁场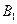 和
和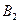 同时以恒定速度沿导轨向右匀速运动时,金属框也会沿导轨向右运动。已知两导轨间距
同时以恒定速度沿导轨向右匀速运动时,金属框也会沿导轨向右运动。已知两导轨间距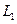 ="0." 4 m,两种磁场的宽度均为
="0." 4 m,两种磁场的宽度均为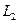 ,
,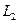 =ab,
=ab,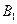 =
=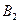 ="1.0" T。金属框的质量m="0." 1 kg,电阻R="2." 0Ω。设金属框受到的阻力与其速度成正比,即
="1.0" T。金属框的质量m="0." 1 kg,电阻R="2." 0Ω。设金属框受到的阻力与其速度成正比,即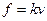 ,比例系数k="0." 08 kg/s。求:
,比例系数k="0." 08 kg/s。求:
(1)当磁场的运动速度为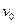 ="5" m/s时,金属框的最大速度
="5" m/s时,金属框的最大速度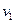 为多大?
为多大?
(2)金属框达到最大速度以后,某时刻磁场停止运动,当金属框的加速度大小为a=4.0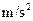 时,其速度
时,其速度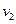 多大?
多大?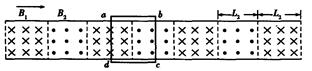
如图所示,在水平面上有两条光滑的长直平行金属导轨MN、PQ,导轨间距离为L,导轨的电阻忽略不计,磁感应强度为B的匀强磁场垂直于导轨所在平面。质量分别为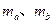 的两根金属杆a、b跨搁在导轨上,接入电路的电阻均为R。轻质弹簧的左端与b杆连接,右端被固定。开始时a杆以初速度
的两根金属杆a、b跨搁在导轨上,接入电路的电阻均为R。轻质弹簧的左端与b杆连接,右端被固定。开始时a杆以初速度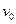 向静止的b杆运动,当a杆向右的速度为v时,b杆向右的速度达到最大值
向静止的b杆运动,当a杆向右的速度为v时,b杆向右的速度达到最大值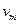 ,此过程中a杆产生的焦耳热为Q,两杆始终垂直于导轨并与导轨良好接触。求当b杆达到最大速度
,此过程中a杆产生的焦耳热为Q,两杆始终垂直于导轨并与导轨良好接触。求当b杆达到最大速度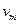 时
时
(1)b杆受到弹簧的弹力。
(2)弹簧具有的弹性势能。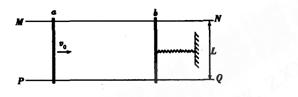
在如图所示的水平导轨上(摩擦、电阻忽略不计),有竖直向下的匀强磁场,磁感强度B,导轨左端的间距为L1=4l0,右端间距为l2=l0。今在导轨上放置ACDE两根导体棒,质量分别为m1=2m0,m2=m0,电阻R1=4R0,R2=R0。若AC棒以初速度V0向右运动,求AC棒运动的过程中产生的总焦耳热QAC,以及通过它们的总电量q。
(07。广东物理卷)如图(a)所示,一端封闭的两条平行光滑导轨相距L,距左端L处的中间一段被弯成半径为H的1/4圆弧,导轨左右两段处于高度相差H的水平面上。圆弧导轨所在区域无磁场,右段区域存在磁场B0,左段区域存在均匀分布但随时间线性变化的磁场B(t),如图(b)所示,两磁场方向均竖直向上。在圆弧顶端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路。从金属棒下滑开始计时,经过时间t0滑到圆弧底端。设金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g。
(1)问金属棒在圆弧内滑动时,回路中感应电流的大小和方向是否发生改变?为什么?
(2)求0到时间t0内,回路中感应电流产生的焦耳热量。
(3)探讨在金属棒滑到圆弧底端进入匀强磁场B0的一瞬间,回路中感应电流的大小和方向。
试题篮
()