高中物理观察电容器的充、放电现象计算题

(12分)质量为、电量为的带电微粒以2m/s的速度从水平放置的平行金属板A、B正中央水平飞入板间，已知板长L=10cm，板间距离d=2cm

（1）若带电微粒恰好沿直线穿过板间，求A、B间的电势差？（g=10m/s²）
（2）当U_AB=2000V时，通过计算判断微粒能否从板间飞出？

如图所示的电路中，R₁＝3 Ω，R₂＝6 Ω，R₃＝1.5 Ω，C＝20 μF，当开关S断开时，电源的总功率为2 W；当开关S闭合时，电源的总功率为4 W，求：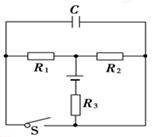

（1）电源的电动势和内电阻；
（2）闭合S时，电源的输出功率；
（3）S断开时，电容器所带的电荷量是多少？

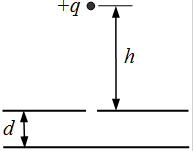
如图所示，充电后的平行板电容器水平放置，电容为，极板间的距离为，上板正中有一小孔。质量为、电荷量为的小球从小孔正上方高h处由静止开始下落，穿过小孔到达下极板处速度恰为零（空气阻力忽略不计，极板间电场可视为匀强电场，重力加速度为）。求：

（1）小球到达小孔处的速度；
（2）极板间电场强度的大小和电容器所带电荷量；
（3）小球从开始下落运动到下极板处的时间。

质量为m的飞机模型，在水平跑道上由静止匀加速起飞，假定起飞过程中受到的平均阻力恒为飞机所受重力的k倍，发动机牵引力恒为F，离开地面起飞时的速度为v，重力加速度为g。求：

（1）飞机模型的起飞距离（离开地面前的运动距离）
（2）若飞机起飞利用电磁弹射技术，将大大缩短起飞距离。图甲为电磁弹射装置的原理简化示意图，与飞机连接的金属块（图中未画出）可以沿两根相互靠近且平行的导轨无摩擦滑动。使用前先给电容为C的大容量电容器充电，弹射飞机时，电容器释放储存电能所产生的强大电流从一根导轨流入，经过金属块，再从另一根导轨流出；导轨中的强大电流形成的磁场使金属块受磁场力而加速，从而推动飞机起飞。
①在图乙中画出电源向电容器充电过程中电容器两极板间电压u与极板上所带电荷量q的图象，在此基础上求电容器充电电压为U₀时储存的电能；
②当电容器充电电压为U_m时弹射上述飞机模型，在电磁弹射装置与飞机发动机同时工作的情况下，可使起飞距离缩短为x。若金属块推动飞机所做的功与电容器释放电能的比值为η，飞机发动的牵引力F及受到的平均阻力不变。求完成此次弹射后电容器剩余的电能。

如图（甲）所示，某粒子源向外放射出一个α粒子，粒子速度方向与水平成30°角，质量为m，电荷量为+q。现让其从粒子源射出后沿半径方向射入一个磁感应强度为B、区域为圆形的匀强磁场（区域Ⅰ）。经该磁场偏转后，它恰好能够沿y轴进入下方的平行板电容器，并运动至N板且恰好不会从N板的小孔P射出电容器。已知平行板电容器与一边长为L的正方形单匝导线框相连，其内有垂直框面的磁场（区域Ⅱ），磁场变化如图（乙）所示。不计粒子重力，求：

（1）磁场区域Ⅱ磁场的方向及α粒子射出粒子源的速度大小；
（2）圆形磁场区域的半径；
（3）α粒子在磁场中运动的总时间。

如图所示的电路，外电阻均为R，电源内阻为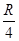.当S断开时，在电容器极板间放一个质量为m，带电荷量为q的电荷恰能静止．当S闭合时，电容器极板间放一个质量仍为m，带电荷量为q′的电荷，恰能静止，则q∶q′为多少．

能的转化与守恒是自然界普遍存在的规律，如：电源给电容器的充电过程可以等效为将电荷逐个从原本电中性的两极板中的一个极板移到另一个极板的过程. 在移动过程中克服电场力做功，电源的电能转化为电容器的电场能．实验表明:电容器两极间的电压与电容器所带电量如图所示．

（1）对于直线运动，教科书中讲解了由v-t图像求位移的方法．请你借鉴此方法，根据图示的Q-U图像，若电容器电容为C，两极板间电压为U，求电容器所储存的电场能．
（2）如图所示，平行金属框架竖直放置在绝缘地面上．框架上端接有一电容为C的电容器．框架上一质量为m、长为L的金属棒平行于地面放置，离地面的高度为h．磁感应强度为B的匀强磁场与框架平面相垂直．现将金属棒由静止开始释放，金属棒下滑过程中与框架接触良好且无摩擦．开始时电容器不带电，不计各处电阻．

求a. 金属棒落地时的速度大小
b. 金属棒从静止释放到落到地面的时间

如图甲所示，在磁感应强度为B的水平匀强磁场中，有两根竖直放置相距为L平行光滑的金属导轨，顶端用一阻直为R的电阻相连，两导轨所在的竖直平面与磁场方向垂直。一根质量为m的金属棒从静止开始沿导轨竖直向下运动，当金属棒下落龙时，速度达到最大，整个过程中金属棒与导轨保持垂直且接触良好。重力加速度为g，导轨与金属棒的电阻可忽略不计，设导轨足够长。求：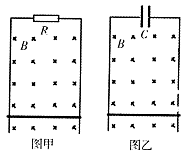

（l）通过电阻R的最大电流；
（2）从开始到速度最大过程中，金属棒克服安培力做的功W_A；
（3）若用电容为C的平行板电容器代替电阻R，如图乙所示，仍将金属棒从静止释放，经历时间t的瞬时速度v₁。

如图所示电路，电源电动势E=12V，内阻r=1Ω。外电路中电阻R₁=2Ω，R₂=3Ω，R₃=7.5Ω。电容器的电容C=2μF。求：

（1）电键S闭合时，电路稳定时电容器所带的电量；
（2）电键从闭合到断开，流过电流表A的电量。

如图甲所示是电容器充、放电电路．配合电流传感器，可以捕捉瞬间的电流变化，并通过计算机画出电流随时间变化的图象．实验中选用直流8 V电源，电容器选用电解电容器．先使单刀双掷开关S与1端相连，电源向电容器充电，这个过程可瞬间完成．然后把单刀双掷开关S掷向2端，电容器通过电阻R放电，传感器将电流传入计算机，图象上显示出放电电流随时间变化的I－t曲线，如图乙所示．以下说法正确的是(　  　)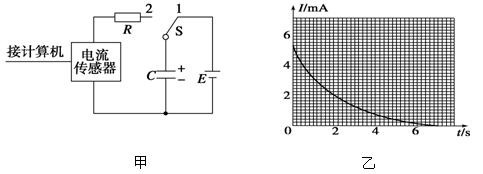

A．电解电容器用氧化膜做电介质，由于氧化膜很薄，所以电容较小

B．随着放电过程的进行，该电容器两极板间电压逐渐减小

C．由传感器所记录的该放电电流图象可以估算出该过程中电容器的放电电荷量

D．通过本实验可以估算出该电容器的电容值

某一平行板电容器两端电压是U，间距为d，设其间为匀强电场，如图所示．现有一质量为m的小球，以速度V₀射入电场，V₀的方向与水平成45°斜向上；要使小球做直线运动，则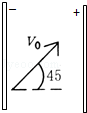

（1）小球带何种电荷？电量是多少？
（2）在入射方向上的最大位移是多少？

在如图所示的电路中，电源电动势E=6.0V，内阻r=2Ω，定值电阻R₁= R₂=10Ω，R₃=30Ω，R₄=35Ω，电容器的电容C=100μF，电容器原来不带电。求：

（1）闭合开关S后，电路稳定时，流过R₃的电流大小I₃；
（2）闭合开关S后，直至电路稳定过程中流过R₄的总电荷量Q．

如图所示，电源电动势E＝12 V，内阻r＝1 Ω，电阻R₁＝3 Ω，R₂＝2 Ω，R₃＝5 Ω，电容器的电容C₁＝4 μF，C₂＝1 μF，求C₁、C₂所带电荷量。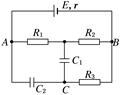

竖直放置的两块足够长的平行金属板间有匀强电场．其电场强度为E，在该匀强电场中，用绝缘丝线悬挂质量为m的带电小球，丝线跟竖直方向成θ=30^o角时小球恰好平衡，且此时与右板的距离为b，如图所示．已知重力加速度为g,求：

（1）小球带电荷量是多少？
（2）若剪断丝线，小球碰到金属板需多长时间？

如图所示，用长L=0.50m的绝缘轻质细线，把一个质量 m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间，平行金属板间的距离d=5.0cm，两板间电压U=1.0×10³V。静止时，绝缘线偏离竖直方向θ角，小球偏离竖直距离a=1.0cm。（θ角很小，为计算方便可认为tanθ ≈ sinθ，取g=10m/s²，需要求出具体数值，不能用θ角表示）求：

（1）两板间电场强度的大小；
（2）判断小球带何种电荷并计算其带电荷量；
（3）在图示位置，若将细线突然剪断，小球做何种性质的运动？求加速度a的大小。