高中物理α粒子散射实验计算题

电子对湮灭是指电子和正电子碰撞后湮灭，产生伽马射线的过程，电子对湮灭是正电子发射计算机断层扫描（PET）及正子湮灭能谱学（PAS）的物理基础．如图所示，在平面直角坐标系xOy上，P点在x轴上，且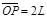，Q点在负y轴上某处．在第Ⅰ象限内有平行于y轴的匀强电场，在第Ⅱ象限内有一圆形区域，与x、y轴分别相切于A、C两点，，在第Ⅳ象限内有一未知的圆形区域（图中未画出），未知圆形区域和圆形区域内有完全相同的匀强磁场，磁场方向垂直于xOy平面向里．一束速度大小为v₀的电子束从A点沿y轴正方向射入磁场，经C点射入电场，最后从P点射出；另一束速度大小为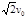的正电子束从Q点沿与y轴正向成45^°角的方向射入第Ⅳ象限，而后进入未知圆形磁场区域，离开磁场时正好到达P点，且恰好与从P点射出的电子束正碰发生湮灭，即相碰时两束粒子速度方向相反．已知正负电子质量均为m、电量均为，电子的重力不计．求：

（1）圆形区域内匀强磁场磁感应强度B的大小和第Ⅰ象限内匀强电场的场强E的大小；
（2）电子从A点运动到P点所用的时间；
（3）Q点纵坐标及未知圆形磁场区域的面积S．

如图所示，竖直平面内有一直角坐标系，在y轴的右侧存在无限大的、场强大小为E、水平向左的匀强电场，在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场Ⅰ．有一不计重力、带正电、比荷为的粒子由＋x轴上某一位置无初速度释放．

（1）若其恰好经过磁场Ⅰ左边界上P点，求粒子射出磁场Ⅰ的速度v₁的大小；
（2）若其恰好经过y轴上的Q点，求粒子从释放开始第一次到达Q所用的时间；
（3）若匀强磁场Ⅰ左侧同时存在一个垂直纸面向里、磁感应强度大小也为B的无限大匀强磁场Ⅱ，要使粒子第二次沿＋x方向运动时恰经过y轴上的M点，试求其在＋x轴上无初速度释放时的位置坐标．

如图（甲）所示，两平行金属板间接有如图（乙）所示的随时间t变化的电压u，两板间电场可看作是均匀的，且两板外无电场，极板长L=0.2m，板间距离d=0.2m，在金属板右侧有一边界为MN的区域足够大的匀强磁场，MN与两板中线OO′垂直，磁感应强度B=5×10^－3T，方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中，已知每个粒子的速度v₀=10⁵m/s，比荷q/m=10⁸C/kg，重力忽略不计，在每个粒子通过电场区域的极短时间内，电场可视作是恒定不变的。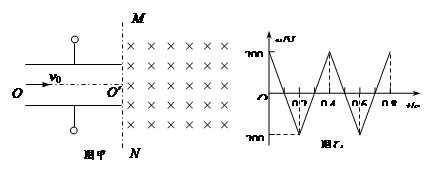

（1）试求带电粒子能够射出电场时的最大电压和对应的射出速度大小。
（2）证明任意时刻从电场射出的带电粒子，进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为定值。
（3）从电场射出的带电粒子，进入磁场运动一段时间后又射出磁场。求粒子在磁场中运动的最长时间和最短时间。

在xoy平面内存在着如图所示的电场和磁场，其中二、四象限内电场方向与y轴平行且相反，大小为E，一、三象限内磁场方向垂直平面向里，大小相等．一个带电粒子质量为m，电荷量为q，从第四象限内的P（L，﹣L）点由静止释放，粒子垂直y轴方向进入第二象限，求：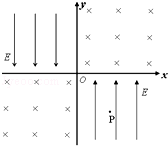

（1）磁场的磁感应强度B；
（2）粒子第二次到达y轴的位置；
（3）粒子从释放到第二次到达y轴所用时间．

如图所示，左侧装置内存在着匀强磁场和方向竖直向下的匀强电场，装置上、下两极板间电势差为U，间距为L；右侧为“台形”匀强磁场区域ACDH，其中，AH//CD，AH=4L。一束电荷量大小为q、质量不等的带电粒子 （不计重力、可视为质点），从狭缝S₁射人左侧装置中恰能沿水平直线运动并从狭缝S₂射出，接着粒子垂直于AH、由AH的中点M射人“台形”区域，最后全部从边界AC射出。若两个区域的磁场方向均水平（垂直于纸面向里）、磁感应强度大小均为B，“台形”宽度MN=L，忽略电场、磁场的边缘效应及粒子间的相互作用。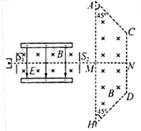

（1）判定这束粒子所带电荷的种类，并求出粒子速度的大小;
（2）求出这束粒子可能的质量最小值和最大值;
（3）求出（2）问中偏转角度最大的粒子在“台形”区域中运动的时间。

如图，在xOy平面的y轴左侧存在沿y轴正方向的匀强电场，y轴右侧区域Ⅰ内存在磁感应强度大小B₁= 匀强磁场，区域Ⅰ、区域Ⅱ的宽度均为L，高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为（– 2L，–L）的A点以速度v₀沿 +x方向射出，恰好经过坐标为[0，-(–1)L]的C点射入区域Ⅰ。粒子重力忽略不计。

（1）求匀强电场的电场强度大小E；
（2）求粒子离开区域Ⅰ时的位置坐标；
（3）要使粒子从区域Ⅱ上边界离开磁场，可在区域Ⅱ内加垂直纸面向内的匀强磁场。试确定磁感应强度B的大小范围，并说明粒子离开区域Ⅱ时的速度方向。

“太空粒子探测器”是由加速、偏转和收集三部分组成，其原理可简化如下：如图1所示，辐射状的加速电场区域边界为两个同心平行半圆弧面，圆心为O，外圆弧面AB的半径为L，电势为φ₁，内圆弧面CD的半径为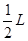，电势为φ₂。足够长的收集板MN平行边界ACDB，O到MN板的距离OP=L。假设太空中漂浮着质量为m，电量为q的带正电粒子，它们能均匀地吸附到AB圆弧面上，并被加速电场从静止开始加速，不计粒子间的相互作用和其它星球对粒子引力的影响。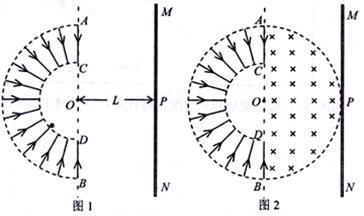

（1）求粒子到达O点时速度的大小；
（2）如图2所示，在边界ACDB和收集板MN之间加一个半圆形匀强磁场，圆心为O，半径为L，方向垂直纸面向内，则发现从AB圆弧面收集到的粒子经O点进入磁场后有2/3能打到MN板上（不考虑过边界ACDB的粒子再次返回），求所加磁感应强度的大小；
（3）同上问，从AB圆弧面收集到的粒子经O点进入磁场后均不能到达收集板MN，求磁感应强度所满足的条件。试写出定量反映收集板MN上的收集效率η与磁感应强度B的关系的相关式子。

如图所示，在矩形区域内有沿纸面向上的匀强电场，场强的大小；在矩形区域内有垂直纸面向里的匀强磁场，磁感应强度大小．已知，．在点处有一放射源，沿纸面向电场中各方向均匀地辐射出速率均为的某种带正电粒子，粒子质量，电荷量，粒子可以无阻碍地通过边界进入磁场，不计粒子的重力．求：

(1)粒子进入磁场的速度大小；
(2)粒子在磁场中做圆周运动的半径；
(3)边界FG上有粒子射出磁场的长度.

如图所示，在倾角为α的光滑斜面上，垂直纸面放置一根长为L、质量为m的直导体棒，导体棒中通有大小为I、方向垂直纸面向里的电流，欲使导体棒静止在斜面上，可以施加方向垂直于导体棒的匀强磁场。求：

（1）若匀强磁场的方向在竖直方向，则磁场方向是向上还是向下？磁感应强度B₁为多大？
（2）若导体棒与斜面间无挤压，则施加的磁场方向如何？则磁感应强度B₂为多大？
（3）沿什么方向施加匀强磁场可使磁感应强度最小？最小值B₃为多少？

如图所示，左侧装置内存在着匀强磁场和方向竖直向下的匀强电场，装置上下两极板间电势差为U，间距为L，右侧为“梯形”匀强磁场区域ACDH，其中，AH//CD， =4L。一束电荷量大小为q、质量不等的带电粒子（不计重力、可视为质点），从狭缝S₁射入左侧装置中恰能沿水平直线运动并从狭缝S₂射出，接着粒子垂直于AH、由AH的中点M射入“梯形”区域，最后全部从边界AC射出。若两个区域的磁场方向均水平（垂直于纸面向里）、磁感应强度大小均为B，“梯形”宽度=L，忽略电场、磁场的边缘效应及粒子间的相互作用。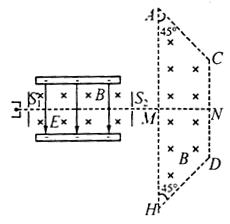

（1）判定这束粒子所带电荷的种类，并求出粒子速度的大小;
（2）求出这束粒子可能的质量最小值和最大值;
（3）求出（2）问中偏转角度最大的粒子在“梯形”区域中运动的时间。

现代科学仪器常利用电场、磁场控制带电粒子的运动。在真空中存在着如图所示的多层紧密相邻的匀强电场和匀强磁场，电场和磁场的宽度均为d。电场强度为E，方向水平向右；磁感应强度为B，方向垂直纸面向里。电场、磁场的边界互相平行且与电场方向垂直，一个质量为m、电荷量为q的带正电粒子在第1层电场左侧边界某处由静止释放，粒子始终在电场、磁场中运动，不计粒子重力及运动时的电磁辐射

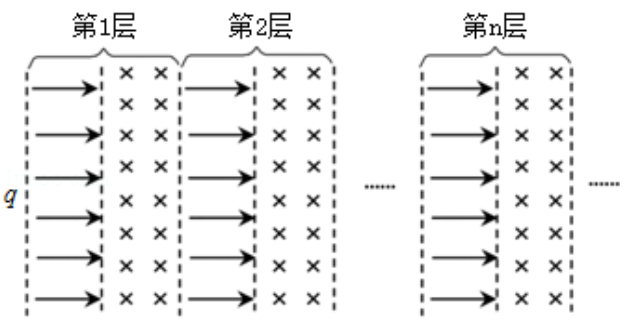
（1）求粒子在第2层磁场中运动时速度 $v_2$ 的大小与轨迹半径 $r_2$ ；

（2）粒子从第n层磁场右侧边界穿出时，速度的方向与水平方向的夹角为 ${\theta }_n$ ，试求 $\sin {\theta }_n$ ；

（3）若粒子恰好不能从第n层磁场右侧边界穿出，试问在其他条件不变的情况下，也进入第n层磁场，但比荷较该粒子大的粒子能否穿出该层磁场右侧边界，请简要推理说明之。

如图所示，一束质量、电荷量的带负电的粒子以某一速率通过一个矩形空间的匀强磁场，磁感应强度B=0.2T；速度方向与磁感线垂直，带电粒子从A点沿AD方向射入，已知AB=DC=0.4m，AD=BC=，求：

（1）若带电粒子的运动速率为，则其在磁场中运动半径R₁为多少？
（2）若带电粒子恰好从C点离开磁场，则其在磁场中运动半径R₂和速率v₂各为多少？

如图所示，两块平行金属极板MN水平放置，板长L="l" m，间距d=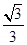m，两金属板间电压U_MN=1×10⁴V；在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域，正三角形ABC内存在垂直纸面向里的匀强磁场，三角形的上顶点A与上金属板M平齐，BC边与金属板平行，AB边的中点P恰好在下金属板N的右端点；正三角形FGH内存在垂直纸面向外的匀强磁场，已知A、F、G处于同一直线上，B、C、H也处于同一直线上，AF两点距离为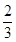m。现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子，粒子质量m=3×l0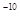kg，带电量q=+l×10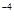C，初速度v₀=1×l0 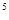m／s。求：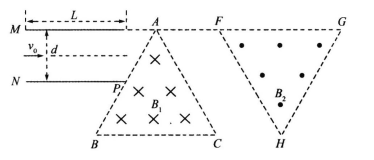

(1)带电粒子从电场中射出时的速度v的大小和方向？
(2)若带电粒子进入三角形区域ABC后垂直打在AC边上，求该区域的磁感应强度 ?
(3)接第(2)问，若要使带电粒子由FH边界进入FGH区域并能再次回到FH界面，求B₂至少应为多大？

如图所示，粒子源O产生初速度为零、电荷量为q、质量为m的正离子，被电压为的加速电场加速后通过直管，在到两极板等距离处垂直射入平行板间的偏转电场，两平行板间电压为2。离子偏转后通过极板MN上的小孔S离开电场。已知ABC是一个外边界为等腰三角形的匀强磁场区域，磁场方向垂直纸面向外，边界AB=AC=L，，离子经过一段匀速直线运动，垂直AB边从AB中点进入磁场。（忽略离子所受重力）
（1）若磁场的磁感应强度大小为B₀，试求离子在磁场中做圆周运动的半径；
（2）若离子能从AC边穿出，试求磁场的磁感应强度大小的范围。

如图所示，在y>0的区域内有沿y轴正方向的匀强电场，在y<0的区域内有垂直坐标平面向里的匀强磁场。一电子（质量为m、电量为e）从y轴上A点以沿x轴正方向的初速度v₀开始运动。当电子第一次穿越x轴时，恰好到达C点；当电子第二次穿越x轴时，恰好到达坐标原点；当电子第三次穿越x轴时，恰好到达D点。C、D两点均未在图中标出。已知A、C点到坐标原点的距离分别为d、2d。不计电子的重力。求

（1）电场强度E的大小；
（2）磁感应强度B的大小；
（3）电子从A运动到D经历的时间t．