高中物理α粒子散射实验试题

如图，在xOy平面的第一、四象限内存在着方向垂直纸面向外，磁感应强度为B的匀强磁场，第四象限内存在方向沿-y方向、电场强度为E的匀强电场．从y轴上坐标为a的一点向磁场区发射速度大小不等的带正电同种粒子，速度方向范围是与+y方向成30°-150°角，且在xOy平面内．结果所有粒子经过磁场偏转后都垂直打到x轴上，然后进入第四象限内的正交电磁场区．已知带电粒子电量为q，质量为m，粒子重力及粒子间相互作用不计．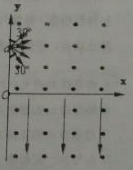

（1）垂直y轴方向射入磁场的粒子的速度大小v₁；
（2）粒子在第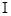象限的磁场中运动的最长时间与最短时间之差；
（3）从x轴上x=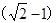a处射入第四象限的粒子穿过电磁场后经过y轴上y=-b的点，求该粒子经过y=-b点的速度大小．

如图所示，用绝缘轻绳悬吊一个带正电的小球，放在匀强磁场中．现把小球拉至悬点右侧a点，轻绳被水平拉直，静止释放后，小球在竖直平面内来回摆动．在小球运动过程中，下列判断正确的是(   )

A．小球摆到悬点左侧的最高点可能比a点高

B．小球每次经过最低点时所受洛伦兹力大小相等

C．小球每次经过最低点时所受洛伦兹力方向相同

D．小球每次经过最低点时轻绳所受拉力大小相等

如图所示，在边界PQ上方有垂直纸面向里的匀强磁场，一对正、负电子同时从边界上的O点沿与PQ成θ角的方向以相同的速度v射入磁场中，则关于正、负电子，下列说法不正确的是

A．在磁场中运动的时间相同	B．在磁场中运动的轨道半径相同
C．出边界时两者的速度相同	D．出边界点到O点处的距离相等

如图所示，半径为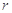的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上A点一粒子源，源源不断地向磁场发射各种方向（均平行于纸面）且速度大小相等的带正电的粒子（重力不计），已知粒子的比荷为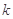，速度大小为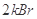。则粒子在磁场中运动的最长时间为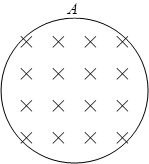

A．

B．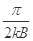

C．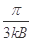

D．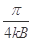

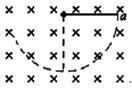
如图所示，有一个正方形的匀强磁场区域abcd，e是ad的中点，f是cd的中点，如果在a点沿对角线方向以速度v射入一带负电的带电粒子，恰好从e点射出，不计粒子重力，则（    ）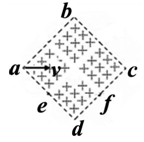

A．如果粒子的速度增大为原来的二倍，将从d点射出

B．如果粒子的速度增大为原来的三倍，将从f点射出

C．如果粒子的速度不变，磁场的磁感应强度变为原来的二倍，将从d点射出

D．只改变粒子的速度使其分别从e、d、f点射出时，从f点射出所用时间最短

如图所示，在真空中坐标xOy面的x＞0区域内，有磁感应强度B=1.0×10^-2T的匀强磁场，方向与xOy平面垂直，在x轴上的P(10,0)点处有一放射源，在xOy平面内向各个方向发射速率为v=1.0×10⁵m/s的带正电粒子，粒子的质量为m=1.0×10^-26kg，粒子带电量为q=1.0×10^-18C，则带电粒子能打到y轴上的范围是（重力的影响不计）（   ）

A．－10cm≤y≤10cm

B．－10cm≤y≤cm

C．cm≤y≤cm

D．cm≤y≤10cm

如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；在x轴下方有一匀强磁场，磁场方向与纸面垂直，一质量为m，电荷量为-q（q>0）的粒子以平行于x轴的速度从y轴上的P点处射入电场，在x轴上的Q点处进入磁场，并从坐标原点O离开磁场，粒子在磁场中的运动轨迹y轴交与M点，已知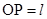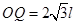，。不计重力，求：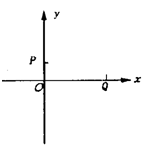

（1）M点与坐标原点O间的距；
（2）粒子从P点运动到M点所用的时间。

在匀强磁场中，一个带电粒子只受洛伦兹力作用做匀速圆周运动，如果又顺利垂直进入另一磁感应强度是原来磁感应强度2倍的匀强磁场中，则（ ）

A．粒子的速率加倍，轨迹半径减半

B．粒子的速率加倍，周期减半

C．粒子的速率减半，轨道半径减半

D．粒子的速率不变，周期减半

如图所示，竖直平面内有一直角坐标系，在y轴的右侧存在无限大的、场强大小为E、水平向左的匀强电场，在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场Ⅰ．有一不计重力、带正电、比荷为的粒子由＋x轴上某一位置无初速度释放．

（1）若其恰好经过磁场Ⅰ左边界上P点，求粒子射出磁场Ⅰ的速度v₁的大小；
（2）若其恰好经过y轴上的Q点，求粒子从释放开始第一次到达Q所用的时间；
（3）若匀强磁场Ⅰ左侧同时存在一个垂直纸面向里、磁感应强度大小也为B的无限大匀强磁场Ⅱ，要使粒子第二次沿＋x方向运动时恰经过y轴上的M点，试求其在＋x轴上无初速度释放时的位置坐标．

如图，一重力不计的带电粒子以一定的速率从a点对准圆心射入一圆形匀强磁场，恰好从b点射出。增大粒子射入磁场的速率，下列判断正确的是（  ）

A．该粒子带正电	B．该粒子带负电
C．粒子从ab间射出	D．粒子从bc间射出

如图所示，在x>O、y>O的空间中有恒定的匀强磁场，磁感应强度的方向垂直于xOy平面向里，大小为B．现有一质量为m、电量为q的带正电粒子，从在x轴上的某点P沿着与x轴成30°角的方向射入磁场。不计重力的影响，则下列有关说法中正确的是

A．粒子在磁场中运动所经历的时间可能为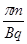
B．粒子在磁场中运动所经历的时间可能为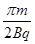
C．只要粒子的速率合适，粒子就可能通过坐标原点
D．粒子一定不可能通过坐标原点

如图所示，以直角三角形AOC为边界的有界匀强磁场区域，磁感应强度为B，∠A＝60°，AO＝L.在O点放置一个粒子源，可以向各个方向发射某种带负电粒子，粒子的比荷为q/m，发射速度大小都为v₀，且满足v₀＝，发射方向由图中的角度θ表示．对于粒子进入磁场后的运动(不计重力作用)，下列说法正确的是

A．粒子有可能打到A点

B．以θ＝60°飞入的粒子在磁场中运动时间最短

C．以θ<30°飞入的粒子在磁场中运动的时间都相等

D．在AC边界上只有一半区域有粒子射出

如图所示，圆形区域存在磁感应强度大小为B，方向垂直纸面向里的匀强磁场，一电荷量为q，质量为m的粒子沿平行于直径AC的方向射入磁场，射入点到直径AC的距离为磁场区域半径的一半，粒子从D点射出磁场时的速率为，不计粒子的重力.求

（1）粒子在磁场中加速度的大小；
（2）粒子在磁场中运动的时间；
（3）圆形区域中匀强磁场的半径.

坐标原点O处有一点状的放射源，它向xoy平面内的x轴上方各个方向发射带正电的同种粒子，速度大小都是v₀，在0<y<d的区域内分布有指向y轴正方向的匀强电场，场强大小为，其中q与m分别为该种粒子的电量和质量；在的区域内分布有垂直于xoy平面的匀强磁场。ab为一块很大的平面感光板，放置于处，如图所示。观察发现此时恰无粒子打到ab板上。（不考虑粒子的重力）

（1）求粒子刚进入磁场时的动能；
（2）求磁感应强度B的大小；
（3）将ab板平移到什么位置时所有粒子均能打到板上?并求出此时ab板上被粒子打中的区域的长度。

（19）许多仪器中可利用磁场控制带电粒子的运动轨迹．在如图所示的真空环境中，有一半径r＝0.05m的圆形区域内存在磁感应强度B＝0.2T的匀强磁场，其右侧相距d＝0.05m处有一足够大的竖直屏．从S处不断有比荷＝1×10⁸C/kg的带正电粒子以速度v＝2×10⁶m/s沿SQ方向射出，经过磁场区域后打在屏上．不计粒子重力．求：
 
(1)粒子在磁场中做圆周运动的轨迹半径；
(2)绕通过P点(P点为SQ与磁场边界圆的交点)垂直纸面的轴，将该圆形磁场区域逆时针缓慢移动90°的过程中，粒子在屏上能打到的范围．