如图,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为,方向垂直于纸面向外,一电荷量为
。质量为
的粒子沿平行于直径
的方向射入磁场区域,射入点与
的距离为
,已知粒子射出磁场与射入磁场时运动方向间的夹角为
,则粒子的速率为(不计重力)()

| A. |
|
B. |
|
C. |
|
D. |
|
图为可测定比荷的某装置的简化示意图,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B,在X轴上距坐标原点L的P处为离子的入射口,在Y上安放接收器,现将一带正电荷的粒子以v的速率从P处射入磁场,若粒子在y轴上距坐标原点L的M处被观测到,且运动轨迹半径恰好最小,设带电粒子的质量为m,电量为q,不计其重力。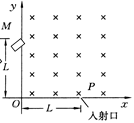
(1)求上述粒子的比荷 ;
;
(2)如果在上述粒子运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其沿y轴正方向做匀速直线运动,求该匀强电场的场强大小和方向;
(3)为了在M处观测到按题设条件运动的上述粒子,在第一象限内的磁场可以局限在一个矩形区域内,求此矩形磁场区域的最小面积。
如图所示,虚线框内为一长方形区域,内有匀强磁场,一束质子以不同的速度从O点垂直磁场方向射入后,分别从a、b、c、d四点射出.比较它们在磁场的运动时间是( )
A. |
B. |
C. |
D. |
如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核( Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿
Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿 方向飞离磁场,N点到O点的距离为L,已知OA间距离为
方向飞离磁场,N点到O点的距离为L,已知OA间距离为 L,α粒子质量为m,电荷量为q,氡核的质量为m0,
L,α粒子质量为m,电荷量为q,氡核的质量为m0,
(1)、写出镭核的衰变方程;
(2)、如果镭核衰变时释放的能量全部变为α粒子和氡核的动能,求一个原来静止的镭核衰变时放出的能量。
如图所示,两块平行金属极板MN水平放置,板长L =1m.间距d= m,两金属板间电压UMN = 1×104 V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上.B、C、H也处于同一直线上.AF两点距离为
m,两金属板间电压UMN = 1×104 V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上.B、C、H也处于同一直线上.AF两点距离为 m。现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m = 3×10-10kg,带电量q = +1×10- 4C,初速度v0=1×105m/s。
m。现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m = 3×10-10kg,带电量q = +1×10- 4C,初速度v0=1×105m/s。
(1)求带电粒子从电场中射出时的速度v的大小和方向
(2)若带电粒子进入中间三角形区域后垂直打在AC边上,求该区域的磁感应强度B1
(3)若要使带电粒子由FH边界进入FGH区域并能再次回到FH界面,求B2应满足的条件
如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v0竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度 ,方向垂直纸面向里。求:
,方向垂直纸面向里。求:
(1)微粒的带电量q;
(2)微粒穿出bc区域的位置到a板下边缘的竖直距离L(用d表示);
(3)微粒在ab、bc区域中运动的总时间t(用d、v0表示)。
如图所示,一质量为m、电量为+q、重力不计的带电粒子,从A板的S点由静止开始释放,经A、B加速电场加速后,穿过中间偏转电场,再进入右侧匀强磁场区域.已知AB间的电压为U,MN极板间的电压为2U,MN两板间的距离和板长均为L,磁场垂直纸面向里、磁感应强度为B、有理想边界.求:
(1)带电粒子离开B板时速度v0的大小;
(2)带电粒子离开偏转电场时速度v的大小与方向;
(3)要使带电粒子最终垂直磁场右边界射出磁场,磁场的宽度d多大?
如图所示,在空间中存在垂直纸面向里的场强为B匀强磁场,其边界AB、CD的宽度为d,在左边界的Q点处有一质量为m,带电量为负q的粒子沿与左边界成30o的方向射入磁场,粒子重力不计.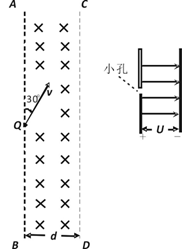
求:
(1)带电粒子能从AB边界飞出的最大速度?
(2)若带电粒子能垂直CD边界飞出磁场,穿过小孔进入如图所示的匀强电场中减速至零且不碰到负极板,则极板间电压及整个过程中粒子在磁场中运动的时间?
(3)若带电粒子的速度是(2)中的 倍,并可以从Q点沿纸面各个方向射入磁场,则粒子能打到CD边界的范围?
倍,并可以从Q点沿纸面各个方向射入磁场,则粒子能打到CD边界的范围?
如图所示,在一底边长为2L,θ=45°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强磁场. 现有一质量为m,电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从O点垂直于AB进入磁场,不计重力与空气阻力的影响。
(1)粒子经电场加速射入磁场时的速度?
(2)磁感应强度B为多少时,粒子能以最大的圆周半径偏转后打到OA板?
如图甲所示,在光滑绝缘的水平桌面上平放着相互平行、间距为0.1m的金属板 、
、 ,板间存在匀强电场,方向水平向右. 在
,板间存在匀强电场,方向水平向右. 在 板右侧平面内存在如图乙所示的交替变化的电磁场. 以
板右侧平面内存在如图乙所示的交替变化的电磁场. 以 板小孔处为坐标原点,建立
板小孔处为坐标原点,建立 坐标系,且规定沿
坐标系,且规定沿 方向为电场的正方向,竖直向下为磁场的正方向. 在
方向为电场的正方向,竖直向下为磁场的正方向. 在 点一质量为10g、电荷量为0.1C的带正电的金属小球由静止释放,设
点一质量为10g、电荷量为0.1C的带正电的金属小球由静止释放,设 时刻金属小球恰好以
时刻金属小球恰好以 m/s的速度经小孔进入
m/s的速度经小孔进入 板右侧. 已知
板右侧. 已知 N/C、
N/C、 =0.2
=0.2 T. 求:
T. 求:
(1) 、
、 两板间的电场强度
两板间的电场强度 的大小;
的大小;
(2)在1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3) 前6s内金属小球运动至离 轴的最远点的位置坐标.(计算结果可以含
轴的最远点的位置坐标.(计算结果可以含 )
)
如图所示的装置可以将比荷不同的粒子分开,图中矩形区域ACDG(AC边足够长)中存在垂直于纸面向里的匀强磁场,磁感应强度大小为 , A处有一宽度为
, A处有一宽度为 的狭缝(宽度大小可调节),两种电性相同的粒子1和粒子2的质量分别是
的狭缝(宽度大小可调节),两种电性相同的粒子1和粒子2的质量分别是 和
和 (
( >
> ),电量的大小均为
),电量的大小均为 ,都以相同的速度
,都以相同的速度 从狭缝各处垂直于GA边且垂直于磁场射入磁场,结果都能落到GA边上,下列说法正确的是( )
从狭缝各处垂直于GA边且垂直于磁场射入磁场,结果都能落到GA边上,下列说法正确的是( )
| A.粒子带正电 |
| B.粒子1一定落在粒子2的左侧 |
C.粒子1落在 边上距狭缝右边缘的最远距离为 边上距狭缝右边缘的最远距离为 |
D.为使两种粒子落在 边上能完全分离,则狭缝的宽度应小于 边上能完全分离,则狭缝的宽度应小于 |
如图所示,xOy为空间直角坐标系,PQ与y轴正方向成θ=30°角。在第四象限和第一象限的xoQ区域存在磁感应强度为B的匀强磁场,在poy区域存在足够大的匀强电场,电场方向与PQ平行,一个带电荷量为+q,质量为m的带电粒子从-y轴上的A(0,-L)点,平行于x轴方向射入匀强磁场,离开磁场时速度方向恰与PQ垂直,粒子在匀强电场中经时间t后再次经过x轴,粒子重力忽略不计。求:(1)从粒子开始进入磁场到刚进入电场的时间t';
(2)匀强电场的电场强度E的大小。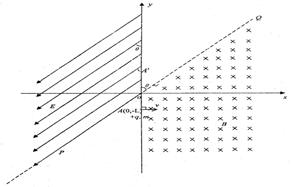
如图所示,两个横截面分别为圆形和正方形的区域内有磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度分别飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入。则下面判断正确的是( )
| A.两电子在两磁场中运动时,其半径一定相同 |
| B.两电子在磁场中运动的时间有可能相同 |
| C.进入圆形磁场区域的电子可能先飞离磁场 |
| D.进入圆形磁场区域的电子可能后飞离磁场 |
如图所示,一束正离子垂直地射入正交的匀强磁场和匀强电场区域里,结果发现有些离子保持原来的运动方向未发生任何偏转.如果让这些不偏转的离子再垂直进入另一匀强磁场中,发现这些离子又分成几束.对这些进入后一磁场的不同轨迹的离子(不计重力),可得出结论:( )
| A.它们的荷质比一定各不相同 |
| B.它们的电量一定各不相同 |
| C.它们的速度大小一定相同 |
| D.它们的质量一定各不相同 |
如图所示,圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子(不计重力)以某一初速度沿圆的直径方向射入磁场,粒子穿过此区域的时间为t,粒子飞出此区域时速度方向偏转60°角,根据上述条件可求下列物理量中的( )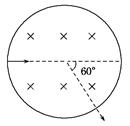
| A.带电粒子的比荷 |
| B.带电粒子的初速度 |
| C.带电粒子在磁场中运动的周期 |
| D.带电粒子在磁场中运动的半径 |
试题篮
()