高中物理计算题

小球A从离地45m高处从静止开始自由下落，同时B球以初速度v₀=20m/s从地面竖直向上抛出，A和B不在同一竖直线上运动，A和B落地后都不反弹，不计空气阻力，g取10m/s²，求：
（1）从A开始下落到A和B在空中处于同一水平高度所需的时间；
（2）当A落地时，B离地高度和速度。

如图1所示，在成都天府大道某处安装了一台500万像素的固定雷达测速仪，可以准确抓拍超速车辆以及测量运动车辆的加速度．一辆汽车正从A点迎面驶向测速仪B，若测速仪与汽车相距355m，此时测速仪发出超声波，同时车由于紧急情况而急刹车，汽车运动到C处与超声波相遇，当测速仪接受到发射回来的超声波信号时，汽车恰好停止于D点，且此时汽车与测速仪相距335m，忽略测速仪安装高度的影响，可简化为如图2所示分析（已知超声波速度为340m/s，）．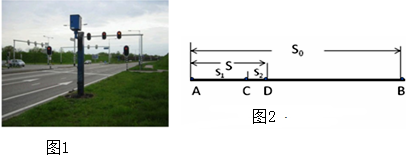

（1）求汽车刹车过程中的加速度a；
（2）此路段有80km/h的限速标志，分析该汽车刹车前的行驶速度是否超速？

如图所示，在边长为a的正方形ABCD的对角线AC左右两侧，分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场， AD、CD是两块固定荧光屏（能吸收打到屏上的粒子）。现有一群质量为m、电量为q的带正电粒子，从A点沿AB方向以不同速率连续不断地射入匀强磁场中，带电粒子速率范围为 。已知，不计带电粒子的重力和粒子之间的相互作用。求：

(1)带电粒子从A点射入到第一次进入电场的时间；
(2)恰能打到荧光屏C D上的带电粒子的入射速度；
(3)CD荧光屏上形成亮线的长度；
(4)AD荧光屏上形成亮线的长度．

中国计划在2017年实现返回式月球软着陆器对月球进行科学探测，届时发射一颗运动半径为r的绕月卫星．登月着陆器从绕月卫星出发，沿椭圆轨道降落到月球的表面上，与月球表面经多次碰撞和弹跳才停下来．假设着陆器第一次弹起的最大高度为h，水平速度为v₁，第二次着陆时速度为v₂．已知月球半径为R，求：在月球表面发射人造月球卫星的最小发射速度．

一质点做匀加速直线运动，初速度为5m/s，加速度为3m/s²．试求该质点：
（1）第5s末的速度；
（2）前5s内的位移；
（3）第5s内的位移．

从离地320m的空中自由落下一个重球，不计阻力，（取g=10m/s²）．求：
（1）经过多少时间落到地面？
（2）从开始落下的时刻起，最后1s内的位移多大？

如图所示，底座A上装有L=0.5m长的直立杆，底座和杆的总质量为M=1.0kg，底座高度不计，杆上套有质量为m=0.2kg的小环B，小环与杆之间有大小恒定的摩擦力．当小环从底座上以v₀=4.0m/s的初速度向上飞起时，恰好能到达杆顶，然后沿杆下降，取g=10m/s²，求：

①在环飞起过程中，底座对水平面的压力；
②此环下降过程需要多长时间．

一物体做匀加速直线运动，初速度为0.5m/s，第7s内的位移比第5s内的位移多4m，求：
（1）物体的加速度；
（2）物体在5s内的位移．

一同学以1m/s的速度沿人行道向公交车站走去，一公交车从身旁的平直公路同向驶过，公交车的速度是15m/s，此时他们距车站的距离为50m．公交车在行驶到距车站25m处开始刹车，刚好到车站停下，停车3s后公交车又启动向前开去．为了安全乘上该公交车，该同学奋力向前跑去，他起跑可看做匀加速直线运动，其加速度大小为2.5m/s²，最大速度是6m/s．求：
（1）若公交车刹车过程视为匀减速直线运动，求公交车刹车过程的加速度大小；
（2）该同学能否在公交车停在车站时追上公交车．

如图所示，为一个实验室模拟货物传送的装置，A是一个表面绝缘质量为2kg的长板车，车置于光滑的水平面上，在车左端放置一质量为1kg带电量为q=1×10^﹣2C的绝缘小货物B，在全部传送途中有一水平匀强电场，可以通过开关控制其有、无及方向．先产生一个方向水平向右，大小E₁=3×10²N/m的电场，车和货物开始运动，作用时间2s后，改变电场，电场大小变为E₂=1×10²N/m，方向向左，电场作用一段时间后，关闭电场，关闭电场时车右端正好到达目的地，货物到达车的最右端，且车和货物的速度恰好为零．已知货物与车间的动摩擦因数µ=0.1，（车不带电，货物体积大小不计，g取10m/s²）求：第二次电场作用的时间。

（1）下列说法正确的是    （填正确答案标号，选对一个得2分，
选对2个得4分，选对3个得5分。每选错一个扣3分，最低得分为0分）

A．将一块晶体敲碎后，得到的小颗粒是非晶体

B．固体可以分为晶体和非晶体两类，有些晶体在不同的方向上有不同的光学性质

C．由同种元素构成的固体，可能会由于原子的排列方式不同而成为不同的晶体

D．在熔化过程中，晶体要吸收热量，但温度保持不变，内能也保持不变

E.在合适的条件下，某些晶体可以转化为非晶体，某些非晶体也可以转化为晶体
（2）如图，气缸左右两侧气体由绝热活塞隔开，活塞与气缸光滑接触。初始时两侧气体均处于平衡态，体积之比V₁:V₂=1:2，温度之比T₁:T₂=2:5。先保持右侧气体温度不变，升高左侧气体温度，使两侧气体体积相同；然后使活塞导热，两侧气体最后达到平衡。求：

①两侧气体体积相同时，左侧气体的温度与初始温度之比；
②最后两侧气体的体积之比。

如图所示，两平行的光滑金属导轨安装在一倾角为α的光滑绝缘斜面上，导轨间距为L，电阻忽略不计且足够长，以宽度为d的有界匀强磁场垂直于斜面向上，磁感应强度为B．另有一长为2d的绝缘杆将一导体棒和一边长为d（d＜L）的正方形线框连在一起组成的固定装置，总质量为m，导体棒中通有大小恒为I的电流．将整个装置置于导轨上，开始时导体棒恰好位于磁场的下边界处．由静止释放后装置沿斜面向上运动，当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零．重力加速度为g．

（1）求刚释放时装置加速度的大小；
（2）求这一过程中线框中产生的热量；
（3）之后装置将向下运动，然后再向上运动，经过若干次往返后，最终整个装置将在斜面上作稳定的往复运动．求稳定后装置运动的最高位置与最低位置之间的距离．

如图，光滑水平面上有一具有光滑曲面的静止滑块B，可视为质点的小球A从B的曲面上离地面高为h处由静止释放，且A可以平稳地由B的曲面滑至水平地面。已知A的质量为m，B的质量为3m，重力加速度为g，试求：

（i）A从B上刚滑至地面时的速度大小；
（ii）若A到地面后与地面上的固定挡板P碰撞，之后以原速率反弹，则A返回B的曲面上能到达的最大高度为多少？

一辆汽车以20m/s的速度沿平直公路从甲地运动到乙地，又以30m/s的速度从乙地运动到丙地．已知甲、乙两地间的距离与乙、丙两地间的距离相等，求汽车从甲地开往丙地的过程中的平均速度．

如图所示是一透明的圆柱体的横截面，其半径为R，折射率为，AB是一条直径，今有一束平行光沿AB方向射向圆柱体，试求距离AB直线多远的入射光线，折射后恰经过B点．