高中物理计算题

一个自由下落的物体，在最后1s内下落的距离为45m。求自由下落的总高度h与总时间t。（g=10m/s²）

如图甲所示，是建筑工地将桩料打入泥土中以加固地基的打夯机示意图。打夯前先将桩料扶正立于地基之上。已知夯锤的质量为M=450kg，桩料的质量为m=50kg。每次打夯都通过卷扬机牵引将夯锤提升到距离桩顶h₀=5m处再释放，让夯锤自由下落，夯锤砸在桩料上并不弹起，而是随桩料一起向下运动。

【两者碰撞时间极短，碰撞前后速度关系满足Mv­₀=(M+m）v】。桩料进入泥土后所受阻力，随打入深度h的变化关系如图乙所示，直线斜率k=5.05×10⁴N／m。每次电动机需用20s的时间提升夯锤。提升夯锤时忽略加速和减速的过程，不计夯锤提升时的动能。g=10m／s²，求

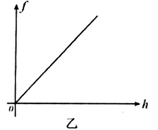
（1）若卷扬机的工作效率为=80％，则在每次提升夯锤的过程中，卷扬机的输入功率。(结果保留2位有效数字）
（2）打完第一夯后，桩料进入泥土的深度。(假设打第一夯前，桩料未进入泥土）

如图所示,将小物体（可视为质点）置于桌面上的薄纸板上,用水平向右的恒力F拉动纸板,拉力大小不同,纸板和小物体的运动情况也不同.若纸板的质量m₁=0.1kg,小物体的质量m₂=0.4kg,小物体与桌面右边缘的距离d=0.12m,与纸板左边缘的距离,已知小物体与纸板上表面以及纸板下表面与桌面的动摩擦因数均为μ=0.2,小物体与桌面的间的动摩擦因数为μ=0.1；设最大静摩擦力与滑动摩擦力相等,g取10m/s².求:

（1）当小物体与纸板一起运动时,桌面给纸板的摩擦力大小;
（2）拉力F满足什么条件,小物体才能与纸板发生相对滑动;
（3）若拉力F作用一段时间t后，纸板从小物体下抽出，从后小物体恰好运动到桌面右边缘停下，求拉力F的大小和作用时间t。

如图所示，P是固定在水平面上的圆弧轨道，O是圆弧的圆心，C为圆弧轨道最高点，D为圆弧轨道最低点。从高台变B点以速度v₀水平飞出质量为m、带电量为+q的小球，恰能从圆弧轨道的左端A点沿圆弧切线方向进入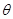，是OA与竖直方向的夹角。圆弧轨道的竖直直径COD右边存在竖直向下的匀强电场，电场强度为E，已知：m=1kg。V0=3m/s，q=，，，g=10m/s2,sin370=0.6， cos370=0.8.若小球恰能到达最高点C，不计空气阻力和所有摩擦，求：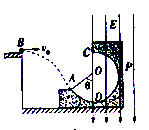

（1）A、B两点的高度差
（2）圆弧轨道的半径R的大小

在游乐场，有一种大型游乐设施跳楼机，参加游戏的游客被安全带固定在座椅上，提升到离地最大高度60m处，然后由静止释放，开始下落过程可认为自由落体运动，下落2s后受到一恒定阻力而做匀减速运动，且下落到地面速度恰好减为零．已知游客和座椅总质量为2000kg，重力加速度g=10m/s²．求：
（1）下落过程中最大速度
（2）该恒定阻力的大小

如图所示，足够长的平行玻璃砖厚度d=3cm，底面镀有反光膜，顶面嵌有涂有遮光物质的挡板AB。一束光线以i=45°的入射角由挡板的A端入射，经底面反射后，恰能从挡板的B端射出。已知光线在玻璃砖中的折射率n=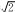，真空中的光速c=3×l0⁸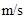，求：

①光线在玻璃中传播的时间t（不考虑光在玻璃砖上表面的反射）
②挡板AB的长度l

如图所示，固定的圆弧轨道与水平面平滑连接，轨道与水平面均光滑，质量为m的物块B与轻质弹簧拴接静止在水平面上，弹簧右端固定.质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放，与B碰撞后推着B一起运动但与B不粘连．求：

①A与B碰前的速度V₀及A、B碰后一起运动的速度V₁；
②弹簧的最大弹性势能；
③A与B第一次分离后，物块A沿圆弧面上升的最大高度．

短跑运动员完成100m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中，某运动用11.00s跑完全程。已知运动员在加速阶段的第2s内通过的距离为7.5m.求:（1）该运动员的加速度；（2）运动员在加速阶段通过的距离。

一个质点从静止开始做匀加速直线运动.已知它在第4s内的位移是14m.求：
（1）质点运动的加速度？
（2）它前进72m所用的时间？

如图所示，水池正上方有一小球，球距水面，池水深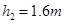，小球从静止释放后落入水中做匀减速运动，到池底的速度恰好为零。（取）求：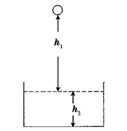

（1）小球运动的最大速度？
（2）从开始到落到池底所用的时间？

某物体做匀加速直线运动，加速度为2 m/s²，通过A点时速度为2m/s，通过B点时速度为6m/s，则：
（1）物体从A点运动到B点的时间为多长？
（2）A、B两点之间的距离是多少？

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来．假设着陆器第一次落到火星表面弹起后，到达最高点时的高度为h，速度方向是水平的，速度大小为v₀，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力．已知火星的一个卫星的圆轨道的半径为r，周期为T．火星可视为半径为r₀的均匀球体．

如图所示，一平板车以某一速度v₀匀速行驶，某时刻一货箱（可视为质点）无初速度地放置于平板车上，货箱离车后端的距离为l=3m，货箱放入车上的同时，平板车开始刹车，刹车过程可视为做a=4m/s²的匀减速直线运动．已知货箱与平板车之间的动摩擦因数为μ=0.2，g=10m/s²．为使货箱不从平板车上掉下来，平板车匀速行驶的速度v₀应满足什么条件？

用磁场可以约束带电离子的轨迹，如图所示，宽d=2cm的有界匀强磁场的横向范围足够大，磁感应强度方向垂直纸面向里，B=1T．现有一束带正电的粒子从O点以v=2×10⁶m/s的速度沿纸面垂直边界进入磁场．粒子的电荷量q=1.6×10^﹣19C，质量m=3.2×10^﹣27kg．求：

（1）粒子在磁场中运动的轨道半径r和运动时间t是多大？
（2）粒子保持原有速度，又不从磁场上边界射出，则磁感应强度最小为多大？

如图，水平放置的光滑的金属导轨M、N，平行地置于匀强磁场中，间距为d，磁场的磁感强度大小为B，方向与导轨平面夹为α，金属棒ab的质量为m，放在导轨上且与导轨垂直．电源电动势为E，内电阻r，定值电阻为R，其余部分电阻不计．则当电键调闭合的瞬间，棒ab的加速度为多大？