用l至9这9个数编制一个三阶幻方,写出所有可能的结果。所谓幻方是指在正方形的方格表的每个方格内填入不同的数,使得每行、每列和两条对角线上的各数之和相等;而阶数是指每行、每列所包含的方格的个数。
某工厂11月份工作忙,星期日不休息,而且从第一天开始,每天都从总厂陆续派相同人数的工人到分厂工作,直到月底,总厂还剩工人240人.如果月底统计总厂工人的
工作量是8070个工作日(一人工作一天为1个工作日),且无人缺勤.那么,这月由总厂派到分厂工作的工人共多少人?
图中共有10个圆圈,6条直线.请问:
(1)能否将l至10填人图中,使得每条直线上各数之和都相等?
(2)能否将0至9填入图中,使得每条直线上各数之和都相等?
(3)请从1至1l中去掉一个数后,将剩下的数填人图中使得每条直线上各数之和都相等.
在下面的图中有11个空的圆圈,要求把1~13这些数填入各圈内(其中3,4已经填好),使得上面两个圆圈内数的和,等于与它相连的下面的圆圈内的数(例如,虚线框中上面两个圈中的数相加,它们的和应等于相连的下面一个圈中的数),并且最下面空着的四圆圈中的数之和等于43.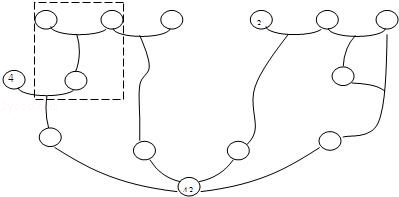
将0,1,2,…,9这10个数分别填人图20﹣30中的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等.这个和最大是多少?最小是多少?请分别给出使得和最大、最小的填法.
将1至9分别填人图中的9个圆圈内,使图中每条直线(图中有7条直线)上的圆圈内所填数之和都相等,那么这个和是多少?
在图中的七个圆圈中填人一些自然数,要求所填的自然数中最小的一个数是1,并且相邻两个圆圈内的数字之差(大数减小数)恰好等于这两个圆圈之间标出的数字.
如图是有名的“六角幻方”:将l到19这19个自然数填人图中的圆圈中,使得每一条直线上圆圈中的各数之和相等,美国数学爱好者阿当斯从l910年开始,到1962年,用了52年的时间才找到了解答.我们给大家填人了6个自然数,请你完成这个“六角幻方”.
请在图的每个空格内填入一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.
如图,大三角形被分成了9个小三角形.试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形三条边的每5个数相加的和相等.这5个数的和最大可能是多少?请给出一种填法.
如图中一共有10个方格,现在把2至11这10个自然数填到里面,每个方格各填一个.如果要求图中的3个2×2的正方形中的4个数之和都相等,那么这个和最小可能是多少?请给出一种填法.
请你将数字1、2、3、4、5、6、7填在图中的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?
请将1个1,2个2,3个3,…,8个8,9个9填人图20.20中,使得相同的数所在的方格都连在一起(相连的两个方格必须有公共边);现在已经给出了其中8个方格中的数,并且知道A、B、C、D、E、F、G各不相同;那么,七位数 是多少?
是多少?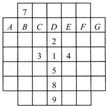
试题篮
()