初中数学试题

设抛物线与x轴的交点为A（， 0），B（，0），其中，点P（m，n）为抛物线上一动点，连接AP，BP．，当∠APB为锐角时，下列m的取值范围中正确的是_________；（填序号）
① m＜-1 ② -1＜m＜0 ③ o＜m＜3 ④ 3＜m＜4 ⑤ m＞4

为了调查某小区居民的用水情况，随机抽查了若干户家庭的月用水量，结果如下表：

则关于这若干户家庭的月用水量，下列说法错误的是（ ）

A．众数是4

B．平均数是4.6

C．调查了10户家庭的月用水量

D．中位数是4.5

（本小题满分10分）某车库出口处设置有“两段式栏杆”，点A是栏杆转动的支点，点E是栏杆两段的连接点，当车辆经过时，栏杆AEF升起后的位置如图1所示（图2为其几何图形）。其中AB⊥BC，DC⊥BC，EF∥BC，∠EAB＝150°，AB＝AE＝1.2m，BC＝2.4m.

（1）求图2中点E到地面的高度（即EH的长。，结果精确到0.01m，栏杆宽度忽略不计）；
（2）若一辆厢式货车的宽度和高度均为2m，这辆车能否驶入该车库？请说明理由.

一组整数3，4，8，5，1，它们的中位数是__________.

已知△ABC∽△DEF，相似比是3：4，则△ABC与△DEF的周长比是__________.

已知反比例函数，当时，，则＝__________.

如下图，在△ABC中，D，E分别是边AB，AC的中点，∠B＝30°。现将△ADE沿DE折叠，点A落在三角形所在平面内的点为A′，则∠BDA′的度数为(    )

A．100°

B．120°

C．130°

D．140°

在学校组织的实践活动中，小王同学用纸板制作了一个圆锥模型，它的底面半径为1，高为，则这个圆锥的侧面积是(    )

A．

B．

C．

D．

－2的倒数是（   ）

A．－2

B．2

C．

D．

如图，已知AB是⊙O的直径，C为⊙O外一点，连结CO并延长交⊙O于点D、E，连结BD并延长交AC于点F，连结AD，∠DAF=∠B．

（1）求证：CA是⊙O的切线；
（2）若AB=6，CA=4，求CD的长；
（3）在（2）的条件下，求tan∠CDF的值．

某中学为了了解本校学生的每周课外阅读时间，采用随机抽样的方式进行了问卷调查，调查结果分为“2小时以内”、“2小时～3小时”、“3小时～4小时”和“4小时以上”四个等级，分别用A、B、C、D表示，根据调查结果绘制成了如图所示的两幅不完整的统计图．由图中所给出的信息解答下列问题：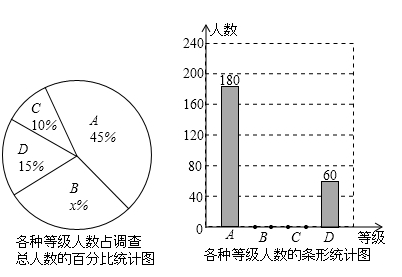

（1）求出x的值，并将不完整的条形图补充完整；
（2）若学校有学生1200人，请你估计每周课外阅读时间在“2小时～3小时”的有多少人？

如图，菱形ABCD中，∠B=120°，AB=2，将图中的菱形ABCD绕点A沿逆时针方向旋转，得菱形AB′C′D′¹，若∠BAD′=110°，在旋转的过程中，点C经过的路线长为       ．

分式的值为0，则x的值为       ．

若正比例函数（）与反比例函数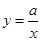（）的图像有两个交点，其中一个交点的坐标为（－3，－2），则另一个交点的坐标为（   ）

A．（2，3）

B．（3，－2）

C．（－2，3）

D．（3，2）

下列计算正确的是（   ）

A．

B．

C．

D．