如图,正方形 的边长为 ,点 , , , 分别在正方形的四条边上,已知 , .
(1)若 ,求四边形 的周长和面积;
(2)求四边形 的周长的最小值.

如图,设 为等腰直角三角形 斜边 上任意一点, 于点 于点 于 点, 交 于点 ,延长 并在其延长线上取一点 ,使得 .求证: ,且 .

下面有四个命题:
(1)一组对边相等且一组对角相等的四边形是平行四边形.
(2)一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形.
(3)一组对角相等且这一组对角的顶点所连接的对角线平分另一条对角线的四边形是平行四边形.
(4)一组对角相等且这一组对角的顶点所连接的对角线被另一条对角线平分的四边形是平行四边形.
上述命题是否正确?正确的请证明,错误的请举出反例.
设直角三角形的两条直角边长分别为 斜边长为 若 均为正数,且 ,求满足条件的直角三角形的个数.
如图,点 是等边三角形 内的一点,连接 ,以 为边作 ,且 ,连接 .
(1)观察并猜想 与 之间的大小关系,并证明你的结论;
(2)若 ,连接 ,试判断 的形状,并说明理由.

恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷 和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路 同侧, 到直线 的距离分别为 和 ,要在沪渝高速公路旁修建一服务区 ,向 两景区运送游客.小民设计了两种方案.图①是方案一的示意图( 与直线 垂直,垂足为 到 的距离之和 ;图②是方案二的示意图(点 关于直线 的对称点是 ,连接 交直线 于点 到 的距离之和 .
(1)求 ,并比较它们的大小;
(2)请你说明 的值为最小;
(3)拟建的恩施到张家界高速公路 与沪渝高速公路垂直,建立如图③所示的直角坐标系, 到直线 的距离为 ,请你在 旁和 旁各修建一服务区 ,使 组成的四边形的周长最小,并求出这个最小值.

先阅读再化简求值.
(1)在化简 的过程中,小王和小李的化简结果不一样.
小王的化简过程如下:
原式 .
小李的化简过程如下:
原式 .
请判断谁的化简结果正确,并说明理由.
(2)化简求值:已知 ,求 的值(结果保留根号).
在等腰梯形 中, ,点 在下底边 上,点 在腰 上.
(1)若 平分等腰梯形 的周长,设 长为 ,试用含 的代数式表示 的面积;
(2)是否存在线段 将等腰梯形 的周长和面积同时平分?若存在,求出此时 的长;若不存在,请说明理由;
(3)是否存在线段 将等腰梯形 的周长和面积同时分成 的两部分?若存在,求出此时 的长;若不存在,请说明理由.

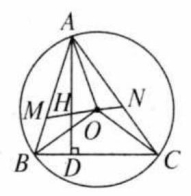
如图,已知 中, 是 的外接圆, 是 边上的高, 是 的垂心,连接 ,连接 并延长交 于点 ,交 于点 ,求证:
(1) ;
(2) 等于 外接圆半径;
(3) .
试题篮
()