初中数学试题

如图，在Rt△ABC中，∠B＝90°，AB＝1，BC＝，以点C
为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．
（1）求AE的长度；
（2）分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，试猜想∠EAG的大小，并说明理由．

 

如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ＝t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．
（1）当t≠1时，求证：△PEQ≌△NFM；
（2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．

 

如图，在平面直角坐标系中，O为坐标原点，P是反比例函数
y＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、
B．
（1）判断P是否在线段AB上，并说明理由；
（2）求△AOB的面积；
（3）Q是反比例函数y＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO
半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．

 

某通讯公司推出①、②两种通讯收费方式供用户选择，其中一
种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间
的函数关系如图所示．
（1）有月租费的收费方式是   （填①或②），
月租费是   元；
（2）分别求出①、②两种收费方式中y与自
变量x之间的函数关系式；
（3）请你根据用户通讯时间的多少，给出
经济实惠的选择建议．

在一个不透明的布袋中装有相同的三个小球，其上面分别标注
数字1、2、3、，现从中任意摸出一个小球，将其上面的数字作为点M的横坐标；将球放回
袋中搅匀，再从中任意摸出一个小球，将其上面的数字作为点M的纵坐标．
（1）写出点M坐标的所有可能的结果；
（2）求点M在直线y＝x上的概率；
（3）求点M的横坐标与纵坐标之和是偶数的概率．

如图，为了测量某建筑物CD的高度，先在地面上用测角仪自
A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处
测得建筑物顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出该建筑物的高度．（取
＝1.732，结果精确到1m）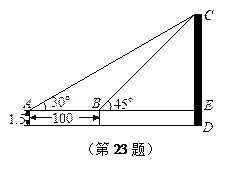
 

省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对
他们进行了六次测试，测试成绩如下表（单位：环）：

	第一次	第二次	第三次	第四次	第五次	第六次
甲	10	8	9	8	10	9
乙	10	7	10	10	9	8

（1）根据表格中的数据，计算出甲的平均成绩是   环，乙的平均成绩是   环；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．
（计算方差的公式：s²＝［］）

已知实数a、b满足ab＝1，a＋b＝2，求代数式a²b＋ab²的值．

解不等式组

计算：．

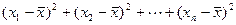一个边长为16m的正方形展厅，准备用边长分别为1m和0.5m的两种正方形地
板砖铺设其地面．要求正中心一块是边长为1m的大地板砖，然后从内到外一圈小地板砖、
一圈大地板砖相间镶嵌（如图所示），则铺好整个展厅地面共需要边长为1m的大地板砖   
块．

如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，
连接BC．若∠A＝26°，则∠ACB的度数为   ．

 

如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所
围的栅栏的总长度是6m．若矩形的面积为4m²，则AB的长度是   m（可利用的围墙长
度超过6m）．

如图，在梯形ABCD中，AB∥DC，∠ADC的平分线与∠BDC的平分线的交点E
恰在AB上．若AD＝7cm，BC＝8cm，则AB的长度是   cm．

 

在平面直角坐标系中，已知点A（－4，0）、B（0，2），现将线段AB向右平移，
使A与坐标原点O重合，则B平移后的坐标是   ．