初中数学试题

如图是六个棱长为1的立方块组成的一个几何体，其俯视图的面积是（　　）

A．6

B．5

C．4

D．3

下列各组数中，互为相反数的是（　　）

A．2和﹣2	B．﹣2和
C．﹣2和	D．和2

．如图，在平面直角坐标系中，已知点A（0,2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角线APQ。当点P运动到原点O处时，记Q得位置为B。
（1）求点B的坐标；
（2）求证：当点P在x轴上运动（P不与Q重合）时，∠ABQ为定值；
（3）是否存在点P，使得以A、O、Q、B为顶点的四边形是梯形？若存在，请求出P点的坐标；若不存在，请说明理由。

使得函数值为零的自变量的值称为函数的零点。例如，对于函数，令y=0，可得x=1，我们就说1是函数的零点。
己知函数 (m为常数)。
（1）当=0时，求该函数的零点；
（2）证明：无论取何值，该函数总有两个零点；
（3）设函数的两个零点分别为和，且，此时函数图象与x轴的交点分
别为A、B(点A在点B左侧)，点M在直线上，当MA+MB最小时，求直线AM的函数解析式。

如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成。已知天桥高度BC≈4.8米，引桥水平跨度AC=8米。

（1）求水平平台DE的长度；
（2）若与地面垂直的平台立枉MN的高度为3米，求两段楼梯AD与BE的长度之比。
(参考数据：取sin37°=0.60，cos37°=0.80，tan37°=0.75

某工程队承包了某标段全长1755米的过江隧道施工任务，甲、乙两个班组分别从东、西两端同时掘进．已知甲组比乙组平均每天多掘进0．6米，经过5天施工，两组共掘进了45米．
（1）求甲、乙两个班组平均每天各掘进多少米?
（2）为加快工程进度，通过改进施工技术，在剩余的工程中，甲组平均每天能比原来多掘进0．2米，乙组平均每天能比原来多掘进0．3米．按此旄工进度，能够比原来少用多少天完成任务?

如图7，在平面直角坐标系xOy中,一抛物线的顶点坐标是（0,1），且过点（-2,2），平行四边形OABC的顶点A、B在此抛物线上，AB与y轴相交于点M.已知点C的坐标是（-4,0），点Q（x,y）是抛物线上任意一点.
（1）  求此抛物线的解析式及点M的坐标；
（2）  在x轴上有一点P(t,0），若PQ∥CM，试用x的代数式表示t；
（3）  在抛物线上是否存在点Q,使得的面积是的面积的2倍？若存在，求
此时点Q的坐标.

为鼓励学生参加体育锻炼，学校计划拿出不超过3200元的资金购买一批篮球和
排球，已知篮球和排球的单价比为3:2，单价和为160元.
（1）篮球和排球的单价分别是多少元？
（2）若要求购买的篮球和排球的总数量是36个，且购买的排球数少于11个，有哪几种购买方案？

如图6，AB是⊙O的直径，BC⊥AB于点B，连接OC交⊙O于   
点E，弦AD∥OC．
(1)求证：      ；
(2)求证：CD是⊙O的切线．

 

 
（图6）

某县为了了解“十、一”国庆期间该县常住居民的出游情况，有关部门随机调查了1600名常住居民，并根据调查结果绘制了如下统计图：

 
根据以上信息，解答下列各题：
(1)补全条形统计图，在扇形统计图中，直接填入出游主要目的是采集发展信息的人数的百分数；
(2)若该县常住居民共48万人，请估计该县常住居民中，利用“十、一”期间出游采集发展信息的人数；
(3)综合上述信息，用一句话谈谈你的感想.

如图5，在A岛周围25海里水域有暗礁，一轮船由西向东航行到O处时，发现A岛在北偏东 $60°$°方向，轮船继续前行20海里到达B处发现A岛在北偏东 $45°$方向，该船若不改变航向继续前进，有无触礁的危险？ （参考数据： $\sqrt{3}\approx 1.732$）

在△ABC和△DEF中，∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤，其正面分别写有五个不同的等式，小民将这五张纸牌背面朝上洗匀后先随机摸出一张（不放回），再随机摸出一张．请结合以上条件，解答下列问题．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用①、②、③、④、⑤表示）；
（2）用两次摸牌的结果和∠C=∠F=90°作为条件，求能满足△ABC和△DEF全等的概率．

给出下列命题：
命题1：直线与双曲线有一个交点是（1，1）；
命题2：直线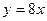与双曲线有一个交点是（，4）；
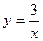命题3：直线与双曲线有一个交点是（，9）；
命题4：直线与双曲线有一个交点是（，16）；
……………………………………………………
（1）请你阅读、观察上面命题，猜想出命题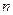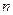（为正整数）；
（2）请验证你猜想的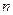命题是真命题．

我市某建筑工地，欲拆除该工地的一危房AB(如图)，准备对该危房实施定向爆破．已知距危房AB水平距离60米（BD＝60米）处有一居民住宅楼，该居民住宅楼CD高15米，在该该住宅楼顶C处测得此危房屋顶A的仰角为30°，请你通过计算说明在实施定向爆破危房AB时，该居民住宅楼有无危险？(在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域，参考数据:，)

（1）计算：
（2）先化简，再求值：，其中．