(本题12分)为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
| 型号 |
占地面积 (单位:m2/个 ) |
使用农户数 (单位:户/个) |
造价 (单位: 万元/个) |
| A |
15 |
18 |
2[ |
| B |
20 |
30 |
3 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)满足条件的方案共有几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).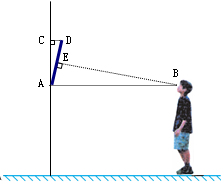
如图,在平面直角坐标系中,直线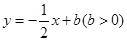 分别交
分别交 轴,
轴,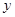 轴于
轴于 两点,以
两点,以 为边作矩形
为边作矩形 ,
,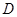 为
为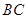 的中点.以
的中点.以 ,
, 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形 ,点
,点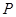 在第一象限,设矩形
在第一象限,设矩形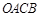 与
与 重叠部分的面积为
重叠部分的面积为 .
.
求点
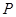 的坐标;
的坐标;当
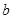 值由小到大变化时,求
值由小到大变化时,求 与
与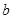 的函数关系式;
的函数关系式;若在直线
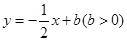 上存在点
上存在点 ,使
,使 等于
等于 ,请直接写出
,请直接写出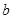 的取值范围
的取值范围在
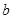 值的变化过程中,若
值的变化过程中,若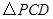 为等腰三角形,且PC=PD,请直接写出
为等腰三角形,且PC=PD,请直接写出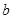 的值.
的值.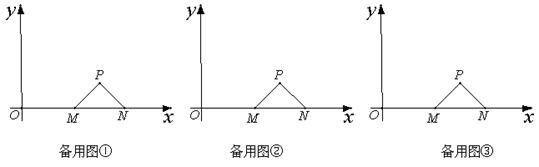
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为 ,
,
直线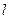 :
: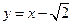 与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与
与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与
轴相切于点M.
求点A的坐标及∠CAO的度数
⊙B以每秒1个单位长度的速度沿
 轴向右平移,同时,直线
轴向右平移,同时,直线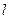 绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线
绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线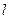 也恰好与⊙B第一次相切,问:直线
也恰好与⊙B第一次相切,问:直线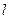 绕点A
绕点A
每秒旋转多少度?如图2,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,
当点E在劣弧AO上运动时(不与A、O两点重合), 的值是否发生变化?如
的值是否发生变化?如
果不变,求其值;如果变化,说明理由.
右图中,ABCD是梯形,面积是1。已知 =
=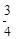 ,
,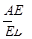 =
= ,
, =
=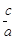 。问:
。问:
(1) 三角形ECD的面积是多少?
(2) 四边形EHFG的面积是多少?
如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,
且ÐAPQ=90°,AQ与BP相交于点T,则 的值为多少?
的值为多少?
循环节长度为2的纯循环小数0.ab可以表示成0.ab= 。
。
若p=0.ab´2009,且p的小数部分是0.12,则0.ab= 。
已知a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,那么a1+a2+a3+…a100= 。
(15届江苏初一1试)一条一条直街上有5栋楼,按从左至右顺序编号为1、2、3、4、5,第k号楼恰好有k(k=1、2、3、4、5)个A厂的职工,相邻两楼之间的距离为50米.A厂打算在直街上建一车站,为使这5栋楼所有A厂职工去车站所走的路程之和最小,车站应建在距1号楼米处.
试题篮
()