一天小莉和妈妈一起逛街,看到某一商场的广告如下:
好消息
为庆祝本店开业25周年,特举办真情回报新老顾客活动,本项活动共设奖金20万元,平均每份奖金200元,特等奖1万元,凡在本店购物满100元者均可参加抽奖,下面是奖金分配一览表:
| 等级 |
特等奖 |
一等奖 |
二等奖 |
三等奖 |
四等奖 |
| 中奖金额 |
10000 |
6000 |
1000 |
50 |
10 |
| 中奖人数 |
3 |
10 |
87 |
350 |
550 |
你认为商场经理说的“平均每份奖金200元”是否欺骗了顾客?这里哪一个数据最能作为中奖金额的代表?
为了了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图(1)、(2)所示的两个统计图(部分未完成).请根据图中信息,回答下列问题: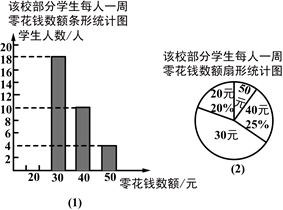
(1)校团委随机调查了多少学生?请你补全条形统计图.
(2)表示“50元”的扇形的圆心角是多少度?被调查的学生每人一周零花钱数额的中位数是多少元?
(3)四川雅安地震后,全校1000名学生每人自发地捐出一周零花钱的一半,以支援灾区建设.请估算全校学生共捐款多少元.
某政府部门招聘公务员1人,对前来应聘的A、B、C三人进行了三项测试,成绩高者将被录用,他们的各项测试成绩如下表所示:
| 测试项目 |
测试成绩 |
||
| A |
B |
C |
|
| 笔试 |
90 |
80 |
75 |
| 面试 |
85 |
85 |
85 |
| 群众评议 |
77 |
84 |
80 |
(1)如果以三项测试的平均成绩为最终成绩确定录用人选,那么谁将被录用?
(2)若将笔试、面试、群众评议三项测试得分按1︰2︰4的比例确定个人的最终成绩,则谁将被录用?
某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
(一)班:168 167 170 165 168 166 171 168 167 170
(二)班:165 167 169 170 165 168 170 171 168 167
(1)完成下面的统计分析表:
| 班级 |
平均数 |
方差 |
中位数 |
极差 |
| (一)班 |
168 |
168 |
6 |
|
| (二)班 |
168 |
3.8 |
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.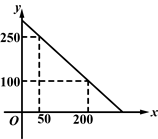
(1)根据图象,求y与x之间的函数关系式.
(2)求甲、乙两种品牌的文具盒的进货单价.
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问:该超市有几种进货方案?哪种方案能使超市获利最大?最大获利为多少元?
某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,供社区居民免费借用.该社区附近A、B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价为3元,目前两家超市同时在做促销活动:
A超市:所有商品均打九折(按标价的90%)销售;
B超市:买一副羽毛球拍送2个羽毛球.
设在A超市购买羽毛球拍和羽毛球的费用为yA(元),在B超市购买羽毛球拍和羽毛球的费用为yB(元).请解答下列问题:
(1)分别写出yA、yB与x之间的关系式.
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.
某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| 空调 |
彩电 |
|
| 进价(元/台) |
5400 |
3500 |
| 售价(元/台) |
6100 |
3900 |
设商场购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x之间的函数关系式.
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示.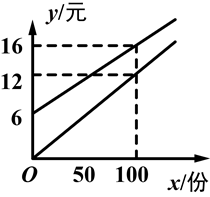
(1)甲种收费方式的函数关系式是________.
乙种收费方式的函数关系式是________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
四川省第十二届运动会将于2014年8月18日在我市隆重开幕,根据大会组委会安排,某校接受了开幕式大型团体操表演任务.为此,学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商,经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元,经洽谈协商:A公司给出的优惠条件是全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女服装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.
(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)、y2(元)与参演男生人数x之间的函数关系式.
(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由.
某校对初中毕业生按综合素质成绩、考试成绩、体育测试成绩三项成绩给学生评定毕业成绩,其权的比为4︰4︰2,毕业成绩达到80分以上(含80分)为优秀毕业生,小明、小亮的三项成绩如下表所示(单位:分):
| 综合素质成绩 |
考试成绩 |
体育测试成绩 |
|
| 满分 |
100 |
100 |
100 |
| 小明 |
72 |
98 |
60 |
| 小亮 |
90 |
75 |
95 |
(1)小明和小亮谁是优秀毕业生?哪位同学的毕业成绩更好些?
(2)升人高中后,请你对他们今后的发展给每人一条建议.
一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
直线y=2x+3与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
试题篮
()