出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:+15,-2.5,+5,-1,+10.5,-3,-2,+12,+4,-5,+6.
(1)若小李出发地记为0,他将最后一名乘客送抵目的地小李距出发地点有多远?
(2)若汽车耗油量为0.4升/ 千米,这天下午小李共耗油多少升?
某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减(单位:个) |
+5 |
-2 |
-5 |
+15 |
-10 |
+16 |
-9 |
(1)写出该厂星期一生产工艺品的数量;
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
某自行车厂计划一周生产自行车2100辆,平均每天计划生产300辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况:(超过每天计划生产数记为正、不足每天计划生产数记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+5 |
﹣1 |
﹣6 |
+13 |
﹣10 |
+15 |
﹣9 |
(1)该厂星期三生产自行车_________辆;
(2)产量最多的一天比产量最少的一天多生产自行车________辆;
(3)该厂本周实际每天平均生产多少辆自行车?
(1)计算: .
(2)下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.
第一步
第二步
第三步
第四步
第五步
第六步
任务一:填空:
①以上化简步骤中,第 步是进行分式的通分,通分的依据是 .或填为: ;
②第 步开始出现错误,这一步错误的原因是 ;
任务二:请直接写出该分式化简后的正确结果;
任务三:除纠正上述错误外,请你根据平时的学习经验,就分式化简时还需要注意的事项给其他同学提一条建议.
某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
| 与标准质量的差值 (单位:g) |
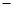 5 5 |
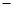 2 2 |
0 |
1 |
3 |
6 |
| 袋 数 |
1 |
4 |
3 |
4 |
5 |
3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下: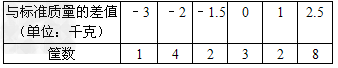
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
阅读以下材料:
苏格兰数学家纳皮尔 . , 年)是对数的创始人.他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得 .
又 ,
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ,② ,③ ;
(2)求证: , , , ;
(3)拓展运用:计算 .
观察以下等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: .
第5个等式: .
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第 个等式: (用含 的等式表示),并证明.
用※定义一种新运算:对于任意实数 和 ,规定 ※ ,如:1※ .
(1)求 ※ ;
(2)若3※ ,求 的取值范围,并在所给的数轴上表示出解集.
已知两个有理数: 和5.
(1)计算: ;
(2)若再添一个负整数 ,且 ,5与 这三个数的平均数仍小于 ,求 的值.
试题篮
()