某检修小组乘一辆检修车沿铁路检修,规定向东走为正,向西走为负,小组的出发地记为0,某天检修完毕时,行走记录(单位:千米)如下:
+10,-2,+3,-1,+9,-3,-2,+11,+3,-4,+6.
(1)问收工时,检修小组距出发地有多远?在东侧还是西侧?
(2)若检修车每千米耗油2.8升,求从出发到收工共耗油多少升?
某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
| 与标准质量的差值 (单位:g) |
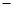 5 5 |
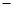 2 2 |
0 |
1 |
3 |
6 |
| 袋 数 |
1 |
4 |
3 |
4 |
5 |
3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
列式并计算:
(1)﹣1减去 的差乘以﹣7的倒数的积;
的差乘以﹣7的倒数的积;
(2)﹣2、5、﹣9这三个数的和的绝对值比这三个数的绝对值的和小多少?
我们规定“*”是一种数学运算符号,两数A、B通过“*”运算得(A+2)×2-B,即A*B=(A+2)×2-B,例如,3*5=(3+2)×2-5=5
(1)求6*7的值;
(2)6*7的值与7*6的值相等吗?
出租车司机小李某天下午的营运全是在东西走向的城中路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:+8, -7, +10, -6,+3,-5,+9,-6
(1)小李下午出发地记为0,他将最后一名乘客送抵目的地时,小李在出发地的什么方向?距下午出发地有多远?
(2)如果汽车耗油量为0.5升/千米,油箱容量为26升,若出发时油箱装满汽油,请你判断途中是否需要补充汽油?
有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下: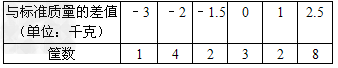
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
阅读以下材料:
苏格兰数学家纳皮尔 . , 年)是对数的创始人.他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得 .
又 ,
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ,② ,③ ;
(2)求证: , , , ;
(3)拓展运用:计算 .
观察以下等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: .
第5个等式: .
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第 个等式: (用含 的等式表示),并证明.
用※定义一种新运算:对于任意实数 和 ,规定 ※ ,如:1※ .
(1)求 ※ ;
(2)若3※ ,求 的取值范围,并在所给的数轴上表示出解集.
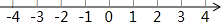
已知两个有理数: 和5.
(1)计算: ;
(2)若再添一个负整数 ,且 ,5与 这三个数的平均数仍小于 ,求 的值.
某地区高山的温度从山脚开始每升高100m降低0.6℃,现测得山脚的温度是4℃.
(1)求离山脚1200m高的地方的温度.
(2)若山上某处气温为-5℃,求此处距山脚的高度.
观察下列各式:
13+23= ;
;
13+23+33=36= ;
;
13+23+33+43=100= ;
;
(1)计算:13+23+33+43+53的值;
(2)计算:13+23+33+43+…+103的值;
(3)猜想:13+23+33+43+…+n3的值.
试题篮
()