如图①,一条笔直的公路上有A、B、C 三地 ,B、C 两地相距150千米,甲、乙两辆汽车分别从
,B、C 两地相距150千米,甲、乙两辆汽车分别从
B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A地的距离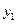 、
、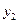 (千米)与行驶时间x(时)的关系如图②所示.
(千米)与行驶时间x(时)的关系如图②所示.
根据图象②进行以下探究: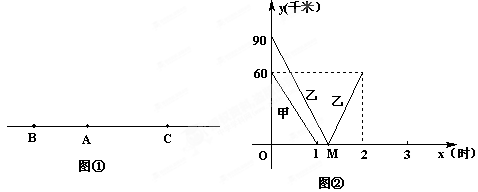
求图中②M点的坐标,并解释该点的实际意义.
在图②中补全甲车的函数图象,求甲车到A地的距离
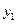 与行驶时间x的函数关系式.
与行驶时间x的函数关系式.A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
如图,直线 轴于点
轴于点 ,直线
,直线 轴于点
轴于点 ,直线
,直线 轴于点
轴于点 ,…直线
,…直线 轴于点
轴于点 .函数
.函数 的图象与直线
的图象与直线 ,
, ,
, ,…
,… 分别交于点
分别交于点 ,
, ,
, ,…
,… ;函数
;函数 的图象与直线
的图象与直线 ,
, ,
, ,…
,… 分别交于点
分别交于点 ,
, ,
, ,…
,… .如果
.如果 的面积记作
的面积记作 ,四边形
,四边形 的面积记作
的面积记作 ,四边形
,四边形 的面积记作
的面积记作 ,…四边形
,…四边形 的面积记作
的面积记作 ,那么
,那么 ▲.
▲.
甲、乙两辆摩托车分别从A、B两地出发相向而行,右图中 分别表示甲、乙两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.则下列说法:
分别表示甲、乙两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.则下列说法:
①A、B两地相距24千米; ②甲车比乙车行完全程多用了0.1小时;
③甲车的速度比乙车慢8千米/小时;④两车出发后,经过小时两车相遇.
其中正确的有( ▲ )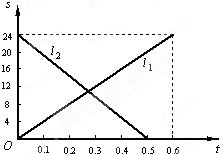
A.1个 B. 2个 C. 3个 D.4个
如图1,已知抛物线的顶点为 ,且经过原点
,且经过原点 ,与
,与 轴的另一个交点为
轴的另一个交点为 .
.求抛物线的解析式;
若
 点
点 在抛物线的对称轴上,点
在抛物线的对称轴上,点 在抛物线上,且以
在抛物线上,且以 、
、 、
、 、
、 四点为
四点为 顶点的四边形为平行四边形,求
顶点的四边形为平行四边形,求 点的坐标;
点的坐标;连接
 、
、 ,如图2,在
,如图2,在 轴下方的抛物线上是否存在点
轴下方的抛物线上是否存在点 ,使得
,使得 与
与 相似?若存在,求出
相似?若存在,求出 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
研究表明一种培育后能繁殖的细胞在一定的环境下有以下规律:若有 个细胞,经过第一周期后,在第1 个周期内要死
个细胞,经过第一周期后,在第1 个周期内要死 去1个,会新繁殖(
去1个,会新繁殖( )个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖(
)个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖( )个;以此类推.例如, 细胞经过第
)个;以此类推.例如, 细胞经过第 个周期后时
个周期后时 ,在第
,在第 个周期内要死去
个周期内要死去 个,又会新繁殖 (
个,又会新繁殖 ( )个.
)个.
(Ⅰ)设在第 周期后时,该细胞的总个数为
周期后时,该细胞的总个数为 ,则
,则 与
与 的关系式为_____.
的关系式为_____.
(Ⅱ) 当 =21时,细胞在第_____周期后时细胞的总个数最多,最多是 个.
=21时,细胞在第_____周期后时细胞的总个数最多,最多是 个.
由函数 图像得到直线y=
图像得到直线y= ,就是将直线y=
,就是将直线y= ( )
( )
| A.向上平移2个单位 | B.向右平移2个单位 |
C.向上平移 个单位 个单位 |
D.向下平移 个单位 个单位 |

物体从足够高的地方做自由落体运动,下降的高度h与时间t满足关系式
则3秒后物体下落的高度是(g取10)……………………………………(▲)
| A.15米 | B.30米 | C.45米 | D.60米 |
如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、
(-1,0)、(1,0)、(-1,-1)。求经过A、B、C三点的抛物线的表达式;
以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。

深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信
息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。求该宾馆共有多少间住房,每间住房每天收费多少元?
通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
已知函数y=x2-2x-2的图象如图1所示,根据其中提供的信息,可求得使
y≥1成立的x的取值范围是( )
| A.-1≤x≤3 | B.-3≤x≤1 | C.x≥-3 | D.x≤-1或x≥3 |
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图像如图所示,根据图中提供的信息,有下列说法:(1)他们都行驶了18千米;(2)甲在途中停留了0. 5 小时;(3)乙比甲晚出发0. 5 小时; (4)相遇后,甲的速度大于乙的速度;(5)甲、乙两人同时到达目的地;(6)乙行驶全程用了1.5小时.其中,符合图象描述的说法有( )
| A.2 个 | B.3 个 | C.4 个 | D.5 个 |

如图(甲),扇形OAB的半径OA=6,圆心角∠AOB=90°,C是 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点H在线段DE上,且EH=
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,图(乙)中表示y与x的函数关系式的图象可能是
DE.设EC的长为x,△CEH的面积为y,图(乙)中表示y与x的函数关系式的图象可能是

试题篮
()