如图,在平面直角坐标系中有一矩形ABCO,B点的坐标为(12,6),点C、A在坐标轴上.⊙A、⊙P的半径均为1,点P从点C开始在线段CO上以1单位/秒的速度向左运动,运动到点O处停止.与此同时,⊙A的半径每秒钟增大2个单位,当点P停止运动时,⊙A的半径也停止变化.设点P运动的时间为t秒.在0<t<12时,设△OAP的面积为s,试求s与t的函数关系式.并求出当t为何值时,s为矩形ABCO面积的
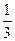 ;
;在点P的运动过程中,是否存在某一时刻,⊙A与⊙P相切,若存在求出点P的坐标,若不存在,说明理由.
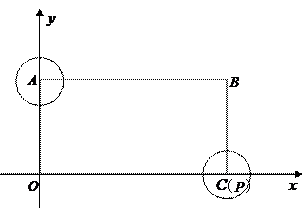
已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )
| A.(3,5) | B.(-5,3) | C.(3,-5) | D.(-5,-3) |
下列函数中,自变量x的取值范围是x≥3的是
A.y=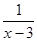 |
B.y=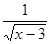 |
C.y="x-3" | D.y= |
在函数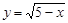 中,自变量x的取值范围是
中,自变量x的取值范围是
| A.x≥5 | B.x≤5 | C.x>5 | D.x<5 |
一个函数的图象如右图,给出以下结论: 
①当 时,函数值最大;
时,函数值最大;
②当 时,函数
时,函数 随
随 的增大而减小;
的增大而减小;
③存在 ,当
,当 时,函数值为0.
时,函数值为0.
其中正确的结论是( )
| A.①② | B.①③ | C.②③ | D.①②③ |
试题篮
()