直线 =
= (k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
(k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
是方程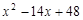 =0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
=0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
秒1个单位长度的速度运动,到达A点时运动停止.直接写出A、B两点的坐标;
设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式;
当S=12时,求出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、
P、M为顶点的四边形是梯形?若存在,请直接写出点M的坐标;若不存在,请说明理由.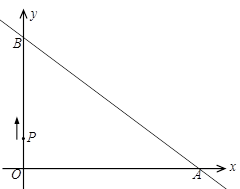
某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的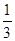 .
.求y与x之间的函数关系式;
由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
温州市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为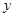 元,试写出
元,试写出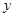 与
与 之间的函数关系式;
之间的函数关系式;若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为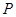 元,试写出
元,试写出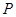 与
与 之间的函数关系式;
之间的函数关系式;李经理将这批野生菌存放多少天后出售可获得最大利润
 元?
元?
(利润=销售总额-收购成本-各种费用)
如图,在直角坐标平面内,函数 (
( ,
, 是常数)
是常数)
的图象经过 ,
, ,其中
,其中 .过点
.过点 作
作 轴垂线,
轴垂线,
垂足为 ,过点
,过点 作
作 轴垂线,垂足为
轴垂线,垂足为 ,连结
,连结 ,
, ,
, .
.
若
 的面积为4,求点
的面积为4,求点 的坐标;
的坐标;若
 ,当
,当 时,求直线
时,求直线 的函数的解析式.
的函数的解析式.
如图,某电信公司提供了 两种方案的移动通讯费用
两种方案的移动通讯费用 (元)与通话时间
(元)与通话时间 (元)之间的关系,则下列结论中
(元)之间的关系,则下列结论中
正确的有
(1)若通话时间少于120分,则 方案比
方案比 方案便宜20元
方案便宜20元
(2)若通话时间超过200分,则 方案比
方案比 方案便宜12元
方案便宜12元
(3)若通讯费用为60元,则 方案比
方案比 方案的通话时间多
方案的通话时间多
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,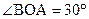
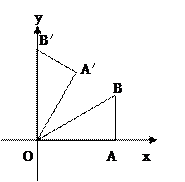
求点B和点A′的坐标;
求经过点B和点B′的直线所对应的一次函数解析式,并判断点A是否在直线BB′上。
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧。
(1) 取BC中点D,问OD+DA是否发生改变,若会,说明理由;若不会,求出OD+DA;(2分。)
(2) 你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;(4分。)
(3) 填空:当OA最长时A的坐标*( , ),直线OA的解析式 。(2分。)

图① 图②备用
让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系。
第一步:数轴上两点连线的中点表示的数
自己画一个数轴,如果点A、B分别表示-2、4,则线段AB的中点M表示的数是 。 再试几个,我们发现:
数轴上连结两点的线段的中点所表示的数是这两点所表示数的平均数。
第二步;平面直角坐标系中两点连线的中点的坐标(如图①)
为便于探索,我们在第一象限内取两点A(x1,y1),B(x2,y2),取线段AB的中点M,分别作A、B到x轴的垂线段AE、BF,取EF的中点N,则MN是梯形AEFB的中位线,故MN⊥x轴,利用第一步的结论及梯形中位线的性质,我们可以得到点M的坐标是( , )(用x1,y1,x2,y2表示),AEFB是矩形时也可以。我们的结论是:平面直角坐标系中连结两点的线段的中点的横(纵)坐标等于这两点的横(纵)坐标的平均数。

图① 图②
第三步:平面直角坐标系中平行四边形的顶点坐标之间的关系(如图②)
在平面直角坐标系中画一个平行四边形ABCD,设A(x1,y1),B(x2,y2),C(x3,y3),
D(x4,y4),则其对角线交点Q的坐标可以表示为Q( , ),也可以表示为Q( , ),经过比较,我们可以分别得出关于x1,x2,x3,x4及,y1,y2,y3,y4的两个等式是 和 。 我们的结论是:平面直角坐标系中平行四边形的对角顶点的横(纵)坐标的 。
已知,如图,在平面直角坐标系xOy中,直线AB与x、y轴分别交于点A( ,0)、B(0,2)。
,0)、B(0,2)。
(1)求直线AB的解析式;(3分。)
(2)求点O到直线AB的距离;(3分。)
(3)求点M(-1,-1)到直线AB的距离。(2分。)
如图,在平面直角坐标系xOy中,点A、B都是直线y=-2x+m(m为常数)上的点,A、B的横坐标分别是-1,2,AC∥y轴,BC∥x轴,则三角形ABC的面积为
A.6 B.9 C.12 D.因m不确定,故面积不确定.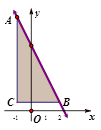
试题篮
()