在平面直角坐标系中,点P(2x-6,x-5)在第四象限,则x的取值范围是( ▲ )
| A.3<x<5 | B.-3<x<5 | C.-5<x<3 | D.-5<x<- 3 3 |
直线 =
= (k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
(k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
是方程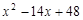 =0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
=0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
秒1个单位长度的速度运动,到达A点时运动停止.直接写出A、B两点的坐标;
设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式;
当S=12时,求出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、
P、M为顶点的四边形是梯形?若存在,请直接写出点M的坐标;若不存在,请说明理由.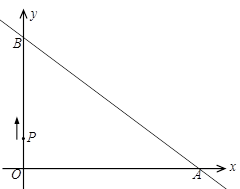
某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的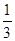 .
.求y与x之间的函数关系式;
由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
温州市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为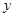 元,试写出
元,试写出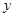 与
与 之间的函数关系式;
之间的函数关系式;若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为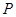 元,试写出
元,试写出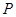 与
与 之间的函数关系式;
之间的函数关系式;李经理将这批野生菌存放多少天后出售可获得最大利润
 元?
元?
(利润=销售总额-收购成本-各种费用)
某文印店,一次性复印收费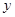 (元)与复印面数(8开纸)
(元)与复印面数(8开纸)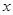 (面)的函数关系如图所示:
(面)的函数关系如图所示: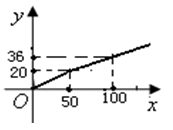
从图象中可看出:复印超过50面的部分每面收费 元,复印200面平均每面收费 元;
两同学各需要复印都不多于50面的资料,他们合起来去该店复印,结果比各自独去复印两人共节省2元钱,问其中一位同学所需复印的面数不能少于多少面?
如图,已知抛物线 经过O(0,0),A(4,0),B(3,
经过O(0,0),A(4,0),B(3, )三点,连接AB,过点B作BC∥
)三点,连接AB,过点B作BC∥ 轴交该抛物线于点C.
轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为
 (秒) (0<
(秒) (0< ≤2),△PQA的面积记为S.
≤2),△PQA的面积记为S.
① 求S与 的函数关系式;
的函数关系式;
② 当 为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的
 值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
试题篮
()