用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)A方法:剪6个侧面;B方法:剪4侧面5个底面.
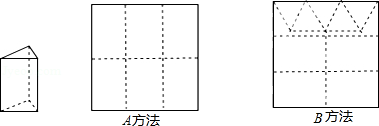
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
①用x的代数式分别表示裁剪出的侧面和底面的个数;
②若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.5m.

(1)按图示规律,第一图案的长度L1=m;第二个图案的长度L2= m;
(2)用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系 ;
规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+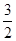 , 3×
, 3×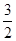
4+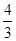 , 4×
, 4×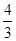
5+ , 5×
, 5× ……, ……
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+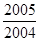 和2005×
和2005×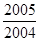 的结果相等吗?
的结果相等吗?
(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃亏?吃亏有多大?(设合适的字母,然后用字母表示)
若一个两位数十位、个位上的数字分别为,
,我们可将这个两位数记为
,易知
;同理,一个三位数、四位数等均可以用此记法,如
.
【基础训练】
(1)解方程填空:
①若,则
;
②若,则
;
③若,则
;
【能力提升】
(2)交换任意一个两位数的个位数字与十位数字,可得到一个新数
,则
一定能被 整除,
一定能被 整除,
一定能被 整除;(请从大于5的整数中选择合适的数填空)
【探索发现】
(3)北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为325,则用,再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.
①该“卡普雷卡尔黑洞数”为 ;
②设任选的三位数为(不妨设
,试说明其均可产生该黑洞数.
观察下面三行数:
-2,4,-8,16,-32,64…;
0,6,-6,18,-30,66…;
1,- ,
, ,-
,- ,
, ,-
,- ,…;
,…;
(1)第一行数的第8个数为 ;
(2)若第一行的第n个数用(-2)n表示,则第三行的第n个数表示为 ;
(3)取每一行的第m个数,三个数的和记为p,
①当m=10时,求p的值;
②当m= 时,|p+30000|的值最小.
某自行车厂计划每天平均生产n辆自行车,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
| 星期 |
一 |
二 |
三 |
四] |
五 |
| 实际生产量 |
+5 |
﹣2 |
﹣4 |
+13 |
﹣3 |
(1)用含n的代数式表示本周前三天生产自行车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=100时,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
我国出租车收费标准因地而异.甲市为:起步价(行驶路程不超过3千米)6元,3千米后每千米(不足1千米,按1千米计算)价格1.5元;乙市为:起步价10元,3千米后每千米价格1.2元.
(1)试问在甲、乙两市乘坐出租车s(s>3)千米的价钱差是多少元?
(2)如果在甲、乙两市乘坐出租车的路程都是10千米,那么哪个市的收费标准高?高多少?
将大小不同的两个正方形按如图所示那样拼接起来,连结BD、BF、DF,已知正方形ABCD的边长为 ,正方形CEFG的边长为
,正方形CEFG的边长为 ,且
,且 <
< .
.

(1)填空:BE×DG = (用含 、
、 的代数式表示);
的代数式表示);
(2)当正方形ABCD的边长 保持不变,而正方形CEFG的边长
保持不变,而正方形CEFG的边长 不断增大时,△BDF的面积会发生改变吗?请说明理由.
不断增大时,△BDF的面积会发生改变吗?请说明理由.
某自行车厂计划每天平均生产n辆自行车,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 实际生产量 |
+5 |
﹣2 |
﹣4 |
+13 |
﹣3 |
(1)用含n的代数式表示本周前三天生产自行车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=100时,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
对于任意一个四位数 ,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数 为"共生数".例如: ,因为 ,所以3507是"共生数"; ,因为 ,所以4135不是"共生数".
(1)判断5313,6437是否为"共生数"?并说明理由;
(2)对于"共生数" ,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记 .求满足 各数位上的数字之和是偶数的所有 .
阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为,排在第二位的数称为第二项,记为
,依此类推,排在第
位的数称为第
项,记为
.所以,数列的一般形式可以写成:
,
,
,
,
,
.
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用表示.如:数列1,3,5,7,
为等差数列,其中
,
,公差为
.
根据以上材料,解答下列问题:
(1)等差数列5,10,15,的公差
为 ,第5项是 .
(2)如果一个数列,
,
,
,
,是等差数列,且公差为
,那么根据定义可得到:
,
,
,
,
,
.
所以
,
,
由此,请你填空完成等差数列的通项公式:
.
(3)是不是等差数列
,
,
的项?如果是,是第几项?
如图,一个点从数轴上的原点开始,先向左移动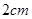 到达
到达 点,再向左移动
点,再向左移动 到达
到达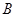 点,然后向右移动
点,然后向右移动 到达
到达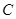 点.
点.
(1)用1个单位长度表示 ,请你在数轴上表示出
,请你在数轴上表示出 、
、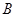 、
、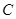 三点的位置;
三点的位置;
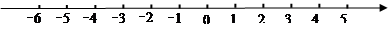
(2)把点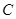 到点
到点 的距离记为
的距离记为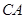 ,则
,则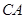 =
= 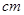 .
.
(3)阅读理解:观察式子: 因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
问题解决
若点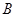 以每秒
以每秒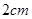 的速度向左移动,同时
的速度向左移动,同时 、
、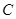 点分别以每秒
点分别以每秒 、
、 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为 秒,试探索:
秒,试探索: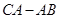 的值是否会随着
的值是否会随着 的变化而改变?请说明理由.
的变化而改变?请说明理由.
试题篮
()