用字母表示有理数的加法运算律.
(1)交换律: ;
(2)结合律: .
一家电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过 分钟的部分免费,超过
分钟的部分免费,超过 分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过
分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过 分钟的部分免费,超过
分钟的部分免费,超过 分钟的按每分钟0.20元收通话费.现在设通话时间是
分钟的按每分钟0.20元收通话费.现在设通话时间是 分钟.
分钟.
(1)当通话时间超过 分钟时,请用含
分钟时,请用含 的代数式表示计费方法A的通话费用.
的代数式表示计费方法A的通话费用.
(2)当通话时间超过 分钟时,请用含
分钟时,请用含 的代数式表示计费方法B的通话费用.
的代数式表示计费方法B的通话费用.
(3)用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?
(4)请你分析,当通话时间超过多少分钟时采用计费方法B合算?
一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把 张这样的餐桌按如图方式拼接起来.
张这样的餐桌按如图方式拼接起来.
(1)问四周可以坐多少人用餐?(用 的代数式表示)
的代数式表示)
(2)若有26人用餐,至少需要多少张这样的餐桌?
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
(1)若设图中最大正方形B的边长是x米,请用含x的代数式表示出正方形F、E和C的边长分别为 , , ;
(2)观察图形可知,长方形相对的两边是相等的(如图中的MN和PQ),请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙两个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?

某市规定如下用水收费标准:每户每月用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.该市某户今年3、4月份的用水量和水费如下表所示:
| 月份 |
用水量(立方米) |
水费(元) |
| 3 |
5 |
7.5 |
| 4 |
9 |
27 |
(1)求出a与b的值;
(2)求当用户用水为x立方米时的水费(用含x的代数式表示);
(3)某用户某月交水费39元,这个月该用户用水多少立方米?
如果某种药降价40%后的价格是a元,则此药的原价是 ( )
| A.(1+40%)a元 | B.(1-40%)a元 |
C.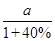 元 元 |
D.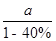 元 元 |
用代数式表示“2m与5的差”为( )
| A.2m-5 | B.5-2m |
| C.2(m-5) | D.2(5-m) |
为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度0.45元收费,如果超过140度,超过部分按每度0.60元收费.
(1)若该住户五月份的用电量是100度,则他五月份应交多少电费?
(2)若该住户六月份的用电量是200度,则他六月份应交多少电费?
(3)若某住户七月份的用电量是 度(
度( >140),求这个用户七月份应交多少电费?(结果用含
>140),求这个用户七月份应交多少电费?(结果用含 的式子表示)
的式子表示)
观察下列等式:
1、42-12=3×5;
2、52-22=3×7;
3、62-32=3×9;
4、72-42=3×11;
…
则第n(n是正整数)个等式为 .
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)认为图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积,
方法① ;方法② .
(3)观察图②,你能写出(m+n)2,(m-n)2,4mn这三个代数式之间的等量关系吗?
(4)根据⑶题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
甲、乙两家文具商店出售同样的钢笔和本子.钢笔每支18元,本子每本2元.甲商店推出的优惠方法为买一支钢笔送两本本子;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支钢笔,本子 本(
本( ≥10)
≥10)
(1)若到甲商店购买,应付 元(用代数式表示).
(2)若到乙商店购买,应付 元(用代数式表示).
(3)若小丽要买本子10本,应选择那家商店?若买100本呢?
试题篮
()