初中数学列代数式试题

由于受 $H7N9$禽流感的影响，我市某城区今年2月份鸡的价格比1月份下降 $a\%$，3月份比2月份下降 $b\%$，已知1月份鸡的价格为24元 $/$千克．设3月份鸡的价格为 $m$元 $/$千克，则 $($　　 $)$

A． $m=24(1-a\%-b\%)$B． $m=24(1-a\%)b\%$

C． $m=24-a\%-b\%$D． $m=24(1-a\%)(1-b\%)$

若一个两位数十位、个位上的数字分别为，，我们可将这个两位数记为，易知；同理，一个三位数、四位数等均可以用此记法，如．

【基础训练】

（1）解方程填空：

①若，则　　；

②若，则　　；

③若，则　　；

【能力提升】

（2）交换任意一个两位数的个位数字与十位数字，可得到一个新数，则一定能被　　整除，一定能被　　整除，一定能被　　整除；（请从大于5的整数中选择合适的数填空）

【探索发现】

（3）北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚．数学中也存在有趣的黑洞现象：任选一个三位数，要求个、十、百位的数字各不相同，把这个三位数的三个数字按大小重新排列，得出一个最大的数和一个最小的数，用得出的最大的数减去最小的数得到一个新数（例如若选的数为325，则用，再将这个新数按上述方式重新排列，再相减，像这样运算若干次后一定会得到同一个重复出现的数，这个数称为“卡普雷卡尔黑洞数”．

①该“卡普雷卡尔黑洞数”为　　；

②设任选的三位数为（不妨设，试说明其均可产生该黑洞数．

四人做传数游戏，甲任报一个数给乙，乙把这个数加１传给丙，丙再把所得的数平方后传给丁，丁把所听到的数减1报出答案：
①若甲报的数为19，则丁的答案是多少？
②请把游戏过程用代数式的程序描述出来。
③若丁报出的答案是35，则甲传给乙的数是多少？

下图方式摆放餐桌和椅子：

（1）1张餐桌可坐4人，2张餐桌可坐     人。
（2）按照上图的方式继续排列餐桌，完成下表。

桌子张数	3	4	n
可坐人数

 

将连续的正整数1，2，3，4，…，排列成如下的数表，用3×3的方框框出9个数（如图）．

（1）图中方框框出的9个数的和与方框正中间的数10有什么关系？
（2）将方框上下左右平移，但一定要框住数表中的9个数．若设正中间的数为a，用含a的代数式表示方框框住的9个数字，并计算这9个数的和．
（3）能否在方框中框出9个数，使这9个数的和为270？若能，求出这9个数；若不能，请说明理由．

某城市出租车收费标准如下：3公里以内（含3公里）收费8元，超过3公里的部分每公里收费1.5元．
（1）若行驶x公里（x为整数），试用含x的代数式表示应收的车费；
（2）若某人乘坐出租汽车行驶8公里，则应付车费多少元？

李克强总理在2015年提出“互联网+”行动计划，随之各领域与互联网+有关的产业应运而生。滴滴专车、神舟专车等专车服务目前已经逐步占据各城市的营运行业的主要营业份额。为了更好的吸引客户群、提高服务品质，“神舟专车”和“滴滴专车”通过不同的收费方式吸引顾客。“神舟专车”决定实施新的收费政策，顾客乘车起步价8元、3公里后，每公里增加1．8元；“滴滴专车”每公里收费2．5元。

（1）若顾客乘坐专车3公里，选择______________（填神舟、滴滴）专车更为合算。
（2）若顾客乘坐专车x公里（x>3），请用含x的代数式分别表示乘坐滴滴专车和神舟专车的收费情况。
（3）若顾客乘坐专车6公里，请你说明选择哪种专车更实惠？

将大小不同的两个正方形按如图所示那样拼接起来，连结BD、BF、DF，已知正方形ABCD的边长为，正方形CEFG的边长为，且＜．

（1）填空：BE×DG =                （用含、的代数式表示）；
（2）当正方形ABCD的边长保持不变，而正方形CEFG的边长不断增大时，△BDF的面积会发生改变吗？请说明理由．

如图，将一张正方形纸片，第1次剪成四个大小形状一样的小正方形，第2次将其中的一个小正方形再按同样的方法剪成四个小正方形，然后再将其中的一个小正方形剪成四个小正方形，如此循环进行下去，如果共剪次，则可剪出_________个正方形．

如图，每一幅图中均含有若干个正方形，第①幅图中含有1个正方形；第②幅图中含有5个正方形；第③幅图中含有14个正方形．按这样的规律下去，则第⑥幅图中含有正方形的个数为（   ）

A．55

B．78

C．91

D．140

阅读下面的材料：

按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．排在第一位的数称为第一项，记为，排在第二位的数称为第二项，记为，依此类推，排在第位的数称为第项，记为．所以，数列的一般形式可以写成：，，，，，．

一般地，如果一个数列从第二项起，每一项与它前一项的差等于同一个常数，那么这个数列叫做等差数列，这个常数叫做等差数列的公差，公差通常用表示．如：数列1，3，5，7，为等差数列，其中，，公差为．

根据以上材料，解答下列问题：

（1）等差数列5，10，15，的公差为　　，第5项是　　．

（2）如果一个数列，，，，，是等差数列，且公差为，那么根据定义可得到：，，，，，．

所以

，

，

由此，请你填空完成等差数列的通项公式：　　．

（3）是不是等差数列，，的项？如果是，是第几项？

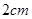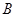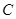如图，一个点从数轴上的原点开始，先向左移动到达点，再向左移动 到达点，然后向右移动到达点．
（1）用1个单位长度表示，请你在数轴上表示出、、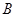三点的位置；

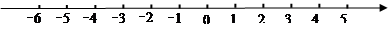
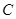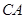（2）把点到点的距离记为，则=       ．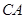
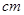（3）阅读理解：观察式子：因此可以得到：括号前面是“－”号，把括号和它前面的“－”号去掉，括号里各项都改变正负号．
问题解决
若点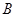以每秒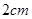的速度向左移动，同时、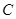点分别以每秒、的速度向右移动．设移动时间为秒,试探索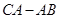：的值是否会随着的变化而改变？请说明理由．

下面每个表格中的四个数都是按相同规律填写的：

根据此规律确定x的值为________．

2011年我国启动“家电下乡”工程，国家对购买家电补贴13%．若某种品牌彩电每台售价a元，则购买时国家补贴（   ）

A．a元

B．13%a元

C．（1－13%）a元

D．（1＋13%）a元

如图所示，已知长方形的长为米,宽为米，半圆半径为米．

（1）这个长方形的面积等于__________平方米；
（2）用代数式表示阴影部分的面积．