某同学化简出现了错误,解答过程如下:
原式 (第一步)
(第二步)
(第三步)
(1)该同学解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
已知:整式,整式
.
尝试 化简整式.
发现,求整式
.
联想 由上可知,,当
时,
,
,
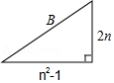
为直角三角形的三边长,如图.填写下表中
的值:
直角三角形三边 |
|||
勾股数组Ⅰ |
8 |
17 |
|
勾股数组Ⅱ |
35 |
|
阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔 . , 年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 ,那么 叫做以 为底 的对数,记作: .比如指数式 可以转化为 ,对数式 可以转化为 .
我们根据对数的定义可得到对数的一个性质: , , , ;理由如下:
设 , ,则 ,
,由对数的定义得
又
解决以下问题:
(1)将指数 转化为对数式 ;
(2)证明 , , ,
(3)拓展运用:计算 .
计算:
(1)7÷(-  )×(
)×( -
-  );
);
(2)2a-3b+[4a-(3a-b)];
(3)(-x2)4+x3·x5-(3x4)2;
(4)(-  )-1+(-2)2×50;
)-1+(-2)2×50;
阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔 . , 年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 ,可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得
又
根据阅读材料,解决以下问题:
(1)将指数式 转化为对数式 ;
(2)求证: , , ,
(3)拓展运用:计算 .
试题篮
()