初中数学一元一次方程的应用试题

2020年5月份，省城太原开展了“活力太原 $·$乐购晋阳”消费暖心活动，本次活动中的家电消费券单笔交易满600元立减128元（每次只能使用一张）．某品牌电饭煲按进价提高 $50\%$后标价，若按标价的八折销售，某顾客购买该电饭煲时，使用一张家电消费券后，又付现金568元．求该电饭煲的进价．

“低碳生活，绿色出行”是一种环保、健康的生活方式，小丽从甲地匀速步行前往乙地，同时，小明从乙地沿同一路线匀速步行前往甲地，两人之间的距离 $y\left(m\right)$与步行时间 $x\left(\mathit{min}\right)$之间的函数关系式如图中折线段 $\mathit{AB}-\mathit{BC}-\mathit{CD}$所示．

（1）小丽与小明出发　　 $\mathit{min}$相遇；

（2）在步行过程中，若小明先到达甲地．

①求小丽和小明步行的速度各是多少？

②计算出点 $C$的坐标，并解释点 $C$的实际意义．

小李读一本名著，星期六读了36页，第二天读了剩余部分的 $\frac{1}{4}$，这两天共读了整本书的 $\frac{3}{8}$，这本名著共有多少页？

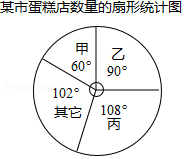
现有甲、乙、丙等多家食品公司在某市开设蛋糕店，该市蛋糕店数量的扇形统计图如图所示，其中统计图中没有标注相应公司数量的百分比．已知乙公司经营150家蛋糕店，请根据该统计图回答下列问题：

（1）求甲公司经营的蛋糕店数量和该市蛋糕店的总数．

（2）甲公司为了扩大市场占有率，决定在该市增设蛋糕店，在其余蛋糕店数量不变的情况下，若要使甲公司经营的蛋糕店数量达到全市的 $20\%$，求甲公司需要增设的蛋糕店数量．

甲、乙两运动员在长为 $100m$的直道 $\mathit{AB}(A$， $B$为直道两端点）上进行匀速往返跑训练，两人同时从 $A$点起跑，到达 $B$点后，立即转身跑向 $A$点，到达 $A$点后，又立即转身跑向 $B$点 $\dots$若甲跑步的速度为 $5m/s$，乙跑步的速度为 $4m/s$，则起跑后 $100s$内，两人相遇的次数为 $($　　 $)$

A．5B．4C．3D．2

光伏发电惠民生，据衢州晚报载，某家庭投资4万元资金建造屋顶光伏发电站，遇到晴天平均每天可发电30度，其它天气平均每天可发电5度，已知某月（按30天计）共发电550度．

（1）求这个月晴天的天数．

（2）已知该家庭每月平均用电量为150度，若按每月发电550度计，至少需要几年才能收回成本（不计其它费用，结果取整数）．

书店举行购书优惠活动：

①一次性购书不超过100元，不享受打折优惠；

②一次性购书超过100元但不超过200元一律打九折；

③一次性购书超过200元一律打七折．

小丽在这次活动中，两次购书总共付款229.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是　　元．

随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位不断增加．

（1）该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个，求该市这两年（从2013年度到2015年底）拥有的养老床位数的平均年增长率；

（2）若该市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间 $(1$个养老床位），双人间 $(2$个养老床位），三人间 $(3$个养老床位），因实际需要，单人间房间数在10至30之间（包括10和 $30)$，且双人间的房间数是单人间的2倍，设规划建造单人间的房间数为 $t$．

①若该养老中心建成后可提供养老床位200个，求 $t$的值；

②求该养老中心建成后最多提供养老床位多少个？最少提供养老床位多少个？

为了美化市容市貌，政府决定将城区旁边一块162亩的荒地改建为湿地公园，规划公园分为绿化区和休闲区两部分．

（1）若休闲区面积是绿化区面积的 $20\%$，求改建后的绿化区和休闲区各有多少亩？

（2）经预算，绿化区的改建费用平均每亩35000元，休闲区的改建费用平均每亩25000元，政府计划投入资金不超过550万元，那么绿化区的面积最多可以达到多少亩？

某市创建“绿色发展模范城市”，针对境内长江段两种主要污染源：生活污水和沿江工厂污染物排放，分别用“生活污水集中处理”（下称甲方案）和“沿江工厂转型升级”（下称乙方案）进行治理，若江水污染指数记为 $Q$，沿江工厂用乙方案进行一次性治理（当年完工），从当年开始，所治理的每家工厂一年降低的 $Q$值都以平均值 $n$计算．第一年有40家工厂用乙方案治理，共使 $Q$值降低了12．经过三年治理，境内长江水质明显改善．

（1）求 $n$的值；

（2）从第二年起，每年用乙方案新治理的工厂数量比上一年都增加相同的百分数 $m$，三年来用乙方案治理的工厂数量共190家，求 $m$的值，并计算第二年用乙方案新治理的工厂数量；

（3）该市生活污水用甲方案治理，从第二年起，每年因此降低的 $Q$值比上一年都增加一个相同的数值 $a$．在（2）的情况下，第二年，用乙方案所治理的工厂合计降低的 $Q$值与当年用甲方案治理降低的 $Q$值相等，第三年，用甲方案使 $Q$值降低了39.5．求第一年用甲方案治理降低的 $Q$值及 $a$的值．

某公司积极开展“爱心扶贫”的公益活动，现准备将6000件生活物资发往 $A$， $B$两个贫困地区，其中发往 $A$区的物资比 $B$区的物资的1.5倍少1000件，则发往 $A$区的生活物资为　       　件．

将正整数1至2018按一定规律排列如下表：

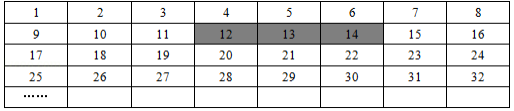
平移表中带阴影的方框，方框中三个数的和可能是 $($　　 $)$

A．2019B．2018C．2016D．2013

我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：

例：将 $0.\dot{7}$化为分数形式

由于 $0.\dot{7}=0.777\dots$，设 $x=0.777\dots$①

则 $10x=7.777\dots$②

② $-$①得 $9x=7$，解得 $x=\frac{7}{9}$，于是得 $0.\dot{7}=\frac{7}{9}$．

同理可得 $0.\dot{3}=\frac{3}{9}=\frac{1}{3}$， $1.\dot{4}=1+0.\dot{4}=1+\frac{4}{9}=\frac{13}{9}$

根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）

（基础训练）

（1） $0.\dot{5}=$　    　， $5.\dot{8}=$　     　；

（2）将 $0.\dot{2}\dot{3}$化为分数形式，写出推导过程；

（能力提升）

（3） $0.\dot{3}1\dot{5}=$　    　， $2.0\dot{1}\dot{8}=$　    　；

（注 $:0.\dot{3}1\dot{5}=0.315315\dots$， $2.0\dot{1}\dot{8}=2.01818\dots )$

（探索发现）

（4）①试比较 $0.\dot{9}$与1的大小： $0.\dot{9}$　    　1（填“ $>$”、“ $<$”或“ $=$” $)$

②若已知 $0.\dot{2}8571\dot{4}=\frac{2}{7}$，则 $3.\dot{7}1428\dot{5}=$　     　．

（注 $:0.\dot{2}8571\dot{4}=0.285714285714\dots )$

一商店在某一时间以每件120元的价格卖出两件衣服，其中一件盈利 $20\%$，另一件亏损 $20\%$，在这次买卖中，这家商店 $($　　 $)$

A．不盈不亏B．盈利20元C．亏损10元D．亏损30元

为配合荆州市“我读书，我快乐”读书节活动，某书店推出一种优惠卡，每张卡售价20元，凭卡购书可享受8折优惠．小慧同学到该书店购书，她先买优惠卡再凭卡付款，结果节省了10元．若此次小慧同学不买卡直接购书，则她需付款多少元？ $($　　 $)$

A．140元B．150元C．160元D．200元