中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.则此人第三天走的路程为
A.96里B.48里C.24里D.12里
列方程解应用题
《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少?
某公司积极开展“爱心扶贫”的公益活动,现准备将6000件生活物资发往 , 两个贫困地区,其中发往 区的物资比 区的物资的1.5倍少1000件,则发往 区的生活物资为 件.
程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是

A.大和尚25人,小和尚75人B.大和尚75人,小和尚25人
C.大和尚50人,小和尚50人D.大、小和尚各100人
直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
我市某校组织爱心捐书活动,准备将一批捐赠的书打包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了16个包还多40本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了9个包,那么这批书共有多少本?
我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 化为分数形式
由于 ,设 ①
则 ②
② ①得 ,解得 ,于是得 .
同理可得 ,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1) , ;
(2)将 化为分数形式,写出推导过程;
(能力提升)
(3) , ;
(注 ,
(探索发现)
(4)①试比较 与1的大小: 1(填“ ”、“ ”或“ ”
②若已知 ,则 .
(注
湖南省2017年公务员录用考试是这样统计成绩的,综合成绩 笔试成绩 面试成绩 ,小红姐姐的笔试成绩是82分,她的竞争对手的笔试成绩是86分,小红姐姐要使自己的综合成绩追平竞争对手,则她的面试成绩必须比竞争对手多
A.2.4分B.4分C.5分D.6分
某超市有线上和线下两种销售方式.与2019年4月份相比,该超市2020年4月份销售总额增长 ,其中线上销售额增长 ,线下销售额增长 .
(1)设2019年4月份的销售总额为 元,线上销售额为 元,请用含 , 的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);
时间 |
销售总额(元 |
线上销售额(元 |
线下销售额(元 |
2019年4月份 |
|
|
|
2020年4月份 |
|
|
|
(2)求2020年4月份线上销售额与当月销售总额的比值.
为配合荆州市“我读书,我快乐”读书节活动,某书店推出一种优惠卡,每张卡售价20元,凭卡购书可享受8折优惠.小慧同学到该书店购书,她先买优惠卡再凭卡付款,结果节省了10元.若此次小慧同学不买卡直接购书,则她需付款多少元?
A.140元B.150元C.160元D.200元
某工厂有甲、乙两个车间,甲车间生产 产品,乙车间生产 产品,去年两个车间生产产品的数量相同且全部售出.已知 产品的销售单价比 产品的销售单价高100元,1件 产品与1件 产品售价和为500元.
(1) 、 两种产品的销售单价分别是多少元?
(2)随着 时代的到来,工业互联网进入了快速发展时期.今年,该工厂计划依托工业互联网将乙车间改造为专供用户定制 产品的生产车间.预计 产品在售价不变的情况下产量将在去年的基础上增加 ; 产品产量将在去年的基础上减少 ,但 产品的销售单价将提高 .则今年 、 两种产品全部售出后总销售额将在去年的基础上增加 .求 的值.
小华输液前发现瓶中药液共250毫升,输液器包装袋上标有"15滴 毫升".输液开始时,药液流速为75滴 分钟.小华感觉身体不适,输液10分钟时调整了药液流速,输液20分钟时,瓶中的药液余量为160毫升.
(1)求输液10分钟时瓶中的药液余量;
(2)求小华从输液开始到结束所需的时间.

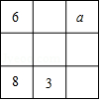
幻方历史悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方.将数字 分别填入如图所示的幻方中,要求每一横行,每一竖行以及两条对角线上的数字之和都是15,则 的值为 .
某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和都是100吨,且甲特产的销售量都不超过20吨.
(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?
(2)求该公司一个月销售这两种特产所能获得的最大总利润.
试题篮
()