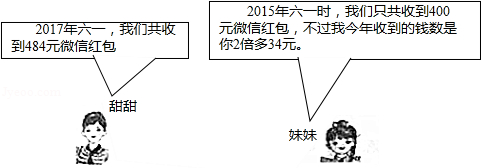
收发微信红包已成为各类人群进行交流联系、增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:(1)2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少钱的微信红包?
某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产每提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;
(2)由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?
某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励.
某服装店以每件30元的价格购进一批 恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设 恤的销售单价提高 元.
(1)服装店希望一个月内销售该种 恤能获得利润3360元,并且尽可能减少库存,问 恤的销售单价应提高多少元?
(2)当销售单价定为多少元时,该服装店一个月内销售这种 恤获得的利润最大?最大利润是多少元?
为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.
巴中市某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4050元的均价开盘销售,若两次下调的百分率相同,求平均每次下调的百分率.
2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
某水果商店销售一种进价为40元 千克的优质水果,若售价为50元 千克,则一个月可售出500千克;若售价在50元 千克的基础上每涨价1元,则月销售量就减少10千克.
(1)当售价为55元 千克时,每月销售水果多少千克?
(2)当月利润为8750元时,每千克水果售价为多少元?
(3)当每千克水果售价为多少元时,获得的月利润最大?
为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2015年该市投入基础教育经费5000万元,2017年投入基础教育经费7200万元.
(1)求该市这两年投入基础教育经费的年平均增长率;
(2)如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2018年用不超过当年基础教育经费的 购买电脑和实物投影仪共1500台,调配给农村学校,若购买一台电脑需3500元,购买一台实物投影需2000元,则最多可购买电脑多少台?
某公司投入研发费用80万元 万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量 销售量),第一年该产品正式投产后,生产成本为6元 件.此产品年销售量 (万件)与售价 (元 件)之间满足函数关系式 .
(1)求这种产品第一年的利润 (万元)与售价 (元 件)满足的函数关系式;
(2)若该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
(3)在(2)的条件下,第二年,该公司将第一年的利润20万元 万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元 件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润 至少为多少万元.
重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称"堂食"小面),也可购买搭配佐料的袋装生面(简称"生食"小面).已知3份"堂食"小面和2份"生食"小面的总售价为31元,4份"堂食"小面和1份"生食"小面的总售价为33元.
(1)求每份"堂食"小面和"生食"小面的价格分别是多少元?
(2)该面馆在4月共卖出"堂食"小面4500份,"生食"小面2500份.为回馈广大食客,该面馆从5月1日起每份"堂食"小面的价格保持不变,每份"生食"小面的价格降低 .统计5月的销量和销售额发现:"堂食"小面的销量与4月相同,"生食"小面的销量在4月的基础上增加 ,这两种小面的总销售额在4月的基础上增加 .求 的值.
今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人.
(1)求四月和五月这两个月中该景区游客人数平均每月增长百分之几;
(2)若该景区仅有 , 两个景点,售票处出示的三种购票方式如下表所示:
| 购票方式 |
甲 |
乙 |
丙 |
| 可游玩景点 |
|
|
和 |
| 门票价格 |
100元 人 |
80元 人 |
160元 人 |
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万,并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
“杂交水稻之父” 袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元.设每天安排 人生产乙产品.
(1)根据信息填表:
产品种类 |
每天工人数(人 |
每天产量(件 |
每件产品可获利润(元 |
甲 |
|
|
15 |
乙 |
|
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润 (元 的最大值及相应的 值.
试题篮
()