初中数学配方法的应用试题

在直角坐标系中，设函数 $y=a{x}^2+\mathit{bx}+1(a$ ， $b$ 是常数， $a\ne 0)$ ．

（1）若该函数的图象经过 $(1,0)$ 和 $(2,1)$ 两点，求函数的表达式，并写出函数图象的顶点坐标；

（2）写出一组 $a$ ， $b$ 的值，使函数 $y=a{x}^2+\mathit{bx}+1$ 的图象与 $x$ 轴有两个不同的交点，并说明理由．

（3）已知 $a=b=1$ ，当 $x=p$ ， $q(p$ ， $q$ 是实数， $p\ne q)$ 时，该函数对应的函数值分别为 $P$ ， $Q$ ．若 $p+q=2$ ，求证： $P+Q>6$ ．

先阅读理解下面的例题，再按要求解答下列问题：
例题 ：求代数式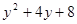的最小值．
解：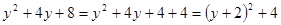
  
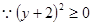
的最小值是．
（1）代数式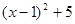的最小值         ；
（2）求代数式的最小值；
（3）某居民小区要在一块一边靠墙（墙长）的空地上建一个长方形花园，花园一边靠墙，另三边用总长为的栅栏围成．如图，设（），请问:当取何值时，花园的面积最大？最大面积是多少？