如图,正方形 边长是 ,点 从点 出发,沿 的路径运动,到 点停止运动,点 从点 出发,在 延长线上向右运动,点 与点 同时出发,点 停止运动时,点 也停止运动,点 ,点 的运动速度都是 ,下列函数图象中能反映 的面积 与运动时间 的函数关系的是

A. B.
B.
C. D.
D.
如图,在 中, , , 于点 ,点 、 、 分别是边 、 、 的中点,连接 、 ,动点 从点 出发,以每秒2个单位长度的速度向点 方向运动,(点 运动到 的中点时停止);过点 作直线 与线段 交于点 ,以 为斜边作 ,点 在 上,设运动的时间为 与矩形 重叠部分的面积为 ,则 与 之间的函数关系图象大致为
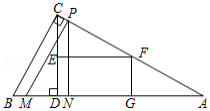
A. B.
B.
C. D.
D.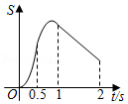
如图,直线 的解析式为 ,它与 轴和 轴分别相交于 , 两点.平行于直线 的直线 从原点 出发,沿 轴的正方向以每秒1个单位长度的速度运动.它与 轴和 轴分别相交于 , 两点,运动时间为 秒 ,以 为斜边作等腰直角三角形 , 两点分别在 两侧).若 和 的重合部分的面积为 ,则 与 之间的函数关系的图象大致是

A. B.
B.
C. D.
D.
如图, 在射线 上顺次取两点 , ,使 ,以 为边作矩形 , ,将射线 绕点 沿逆时针方向旋转, 旋转角记为 (其 中 ,旋转后记作射线 ,射线 分别交矩形 的边 , 于点 , . 若 , ,则下列函数图象中, 能反映 与 之间关系的是

A . B .
B .
C . D .
D .
如图, 的半径为1, , 是 的两条互相垂直的直径,点 从点 出发 点与 点不重合),沿 的路线运动,设 , ,那么 与 之间的关系图象大致是
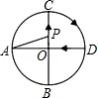
A.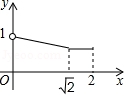 B.
B.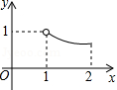
C.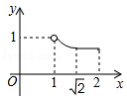 D.
D.
如图,正方形 的边长为 ,动点 从点 出发以 的速度沿着边 运动,到达点 停止运动,另一动点 同时从点 出发,以 的速度沿着边 向点 运动,到达点 停止运动,设点 运动时间为 , 的面积为 ,则 关于 的函数图象是

A. B.
B.
C. D.
D.
如图,正方形 的边长为 ,动点 从点 出发以 的速度沿着边 运动,到达点 停止运动,另一动点 同时从点 出发,以 的速度沿着边 向点 运动,到达点 停止运动,设点 运动时间为 , 的面积为 ,则 关于 的函数图象是
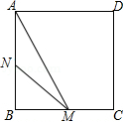
A.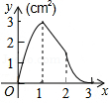 B.
B.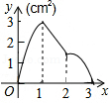
C.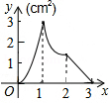 D.
D.
如图,在四边形 中, , , , , 、 、 分别是 、 、 上的点, , ,点 从点 出发,以每秒1个单位长度的速度沿折线 向点 运动,同时点 从点 出发,以相同的速度沿折线 向点 运动,当其中一个点到达后,另一个点也停止运动.设 的面积为 ,运动时间为 秒,则 与 函数关系的大致图象为

A. B.
B.
C. D.
D.
如图,菱形 的边长为2, ,点 和点 分别从点 和点 出发,沿射线 向右运动,且速度相同,过点 作 ,垂足为 ,连接 ,设点 运动的距离为 , 的面积为 ,则能反映 与 之间的函数关系的图象大致为

A. B.
B.
C. D.
D.
如图,等腰直角三角形 , , ,以点 为中心的正方形 边长为 , ,正方形 与等腰直角三角形 重叠部分的面积为 ,则大致能反映 与 之间的函数关系的图象为

A. B.
B.
C. D.
D.
如图,在 中, , , 于点 ,点 为 边上一动点, 交射线 于点 ,作 关于 的轴对称图形得到 ,设 的长为 , 与 重合部分的面积为 .下列图象中,能反映点 从点 向点 运动过程中, 与 的函数关系的是

A. B.
B.
C. D.
D.
如图,已知点 ,点 在 轴正半轴上的一动点,以 为边作等腰直角三角形 ,使点 在第一象限, ,设点 的横坐标为 ,点 的纵坐标为 ,则表示 与 的函数关系的图象大致是

A. B.
B.
C. D.
D.
如图,四边形 是矩形, , ,点 在对角线 上(不与点 , 重合), , 过点 , 交 于点 ,交 于点 , 交 于点 ,交 于点 , 交 于点 .设 , ,则 关于 的函数图象是

A. B.
B.
C. D.
D.
如图,在菱形 中, , ,动点 从点 出发,以每秒1个单位长度的速度沿折线 运动到点 ,同时动点 从点 出发,以相同速度沿折线 运动到点 ,当一个点停止运动时,另一个点也随之停止.设 的面积为 ,运动时间为 秒,则下列图象能大致反映 与 之间函数关系的是

A. B.
B.
C. D.
D.
试题篮
()