如图,已知直线 与坐标轴分别交于 、 两点,那么过原点 且将 的面积平分的直线 的解析式为
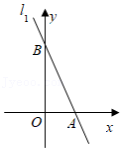
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系 中,有一个由六个边长为1的正方形组成的图案,其中点 , 的坐标分别为 , .若过原点的直线 将这个图案分成面积相等的两部分,则直线 的函数解析式为 .
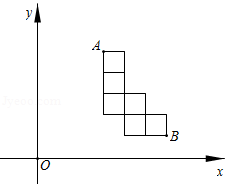
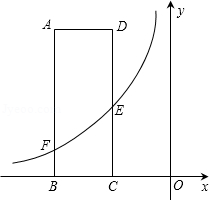
如图,矩形 的两边 、 的长分别为3、8, 是 的中点,反比例函数 的图象经过点 ,与 交于点 .
(1)若点 坐标为 ,求 的值及图象经过 、 两点的一次函数的表达式;
(2)若 ,求反比例函数的表达式.
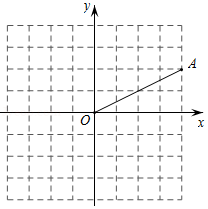
如图,点 的坐标为 .将点 绕坐标原点 旋转 后,再向左平移1个单位长度得到点 ,则过点 的正比例函数的解析式为 .
如图,在平面直角坐标系中,抛物线与
轴交于点
,过点
作
轴的平行线交抛物线于点
.
为抛物线的顶点.若直线
交直线
于点
,且
为线段
的中点,则
的值为 .

试题篮
()